题目内容
a≥0,b≥0,a+b=1,且x1,x2为正数,y1=ax1+bx2,y2=bx1+ax2,则y1y2与x1x2的大小关系是( )
| A、y1y2≥x1x2 |
| B、y1y2≤x1x2 |
| C、y1y2>x1x2 |
| D、y1y2<x1x2 |
考点:不等式比较大小
专题:
分析:将y1、y2代入乘积y1y2展开,化简出x1x2的表达式,判断其大小,即可.
解答:
解:因为a≥0,b≥0,a+b=1 所以1≥a≥0,1≥b≥0
又以为,b=1-a 则(ax1+bx2)(ax2+bx1)
=[x1-b(x1-x2)][x2+b(x1-x2)]
=x1x2+bx1(x1-x2)-bx2(x1-x2)-(b2)(x1-x2)2
=x1x2+b(x1-x2)2-(b2)(x1-x2)2
=x1x2+(b-b2)(x1-x2)2
因为1≥b≥0,所以b≥b2则(b-b2)(x1-x2)2≥0
即:(ax1+bx2)(ax2+bx1)≥x1x2.
故选A.
又以为,b=1-a 则(ax1+bx2)(ax2+bx1)
=[x1-b(x1-x2)][x2+b(x1-x2)]
=x1x2+bx1(x1-x2)-bx2(x1-x2)-(b2)(x1-x2)2
=x1x2+b(x1-x2)2-(b2)(x1-x2)2
=x1x2+(b-b2)(x1-x2)2
因为1≥b≥0,所以b≥b2则(b-b2)(x1-x2)2≥0
即:(ax1+bx2)(ax2+bx1)≥x1x2.
故选A.
点评:比较大小一般是作差法和作商法,本题是中档题.

练习册系列答案
相关题目
已知y=f(x)是偶函数,且在[0,+∞)上是减函数,则f(1-x2)是增函数的区间是( )
| A、[0,+∞) |
| B、(-∞,0] |
| C、[-1,0)∪(1,+∞) |
| D、(-∞,-1]∪(0,1] |
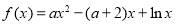 .
.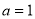 时,求曲线
时,求曲线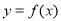 在点
在点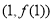 处的切线方程;
处的切线方程;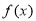 的单调区间;
的单调区间;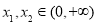 ,
,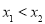 ,且
,且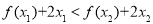 恒成立,求
恒成立,求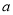 的取值范围.
的取值范围. 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 的面积为
的面积为 ,则
,则 ;
;
 =sin(2x+
=sin(2x+ )+ cos 2x.
)+ cos 2x.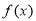 的单调递增区间。
的单调递增区间。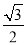 ,a=2,B=
,a=2,B=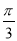 ,求△ABC的面积.
,求△ABC的面积. 中,
中,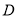 ,
,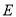 分别是
分别是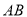 ,
,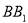 的中点.
的中点. 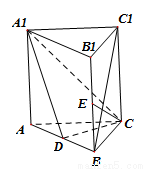
 平面
平面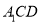 ;
;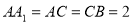 ,
, ,求四棱锥
,求四棱锥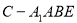 的体积.
的体积.