题目内容
下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（ ）
A、y=
| ||
| B、y=2-|x| | ||
| C、y=1+log2x | ||
| D、y=x2 |
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：根据函数奇偶性和单调性的性质分别进行判断即可．
解答：
解：y=
是奇函数，不满足条件．
y=2-|x|是偶函数，在（0，+∞）上单调递减，不满足条件．
y=1+log2x为非奇非偶函数，不满足条件．
y=x2是偶函数又在区间（0，+∞）上单调递增，满足条件．
| 1 |
| x3 |
y=2-|x|是偶函数，在（0，+∞）上单调递减，不满足条件．
y=1+log2x为非奇非偶函数，不满足条件．
y=x2是偶函数又在区间（0，+∞）上单调递增，满足条件．
点评：本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
练习册系列答案
海淀黄冈名师导航系列答案
相关题目
一个几何体的三视图如图所示，则这个几何体的体积等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若不等式ax2+4ax+8＞0的解集为R，则实数a的取值范围是（ ）
| A、（0，2） |
| B、（-∞，0）∪（2，+∞） |
| C、[0，2） |
| D、（-∞，0]∪（2，+∞） |
函数f（x）=x+
的极值情况是（ ）
| 4 |
| x |
| A、既无极小值，也无极大值 |
| B、当x=-2时，极大值为-4，无极小值 |
| C、当x=2，极小值为4，无极大值 |
| D、当x=-2时，极大值为-4，当x=2时极小值为4 |
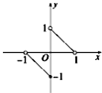定义在[-1，0）∪（0，1]的奇函数f（x），在（0，1]的图象如图，f（x）-f（-x）＞-1的解集是（ ）A、(-1，-
| ||
B、[-1，
| ||
C、(-
| ||
D、(-
|
设f（x）是R上的偶函数，且在（-∞，0）上为减函数，若x1＜0，x1+x2＞0，则（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）=f（x2） |
| C、f（x1）＜f（x2） |
| D、不能确定f（x1）与f（x2）的大小 |