题目内容
18.若$sinθ+cosθ=\frac{17}{13},θ∈(0,\frac{π}{4})$,则tanθ=$\frac{5}{12}$.分析 由已知利用同角三角函数的基本关系求得2sinθcosθ=$\frac{120}{169}$,再根据2sinθcosθ═$\frac{2tanθ}{1+ta{n}^{2}θ}$,即可求得tanθ的值.
解答 解:∵$sinθ+cosθ=\frac{17}{13},θ∈(0,\frac{π}{4})$,
∴1+2sinθcosθ=$\frac{289}{169}$,
∴2sinθcosθ=$\frac{120}{169}$,
∵2sinθcosθ=$\frac{2sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{2tanθ}{1+ta{n}^{2}θ}$=$\frac{120}{169}$,
∴解得:tanθ=$\frac{5}{12}$.
故答案为:$\frac{5}{12}$.
点评 本题主要考查同角三角函数的基本关系、二倍角公式的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
8.已知直线l1:2x+3my-m+2=0和l2:mx+6y-4=0,若l1∥l2,则l1与l2之间的距离为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{10}}{5}$ |
9.已知向量$\overrightarrow a=(1,1,0)$,$\overrightarrow b=(-1,0,2)$,且$k\overrightarrow a+\overrightarrow b$与$\overrightarrow a$互相垂直,则k=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
6.点(x,y)满足$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤4\\ x,y∈N\end{array}\right.$,则点A落在区域C:x2+y2-4x-4y+7≤0内的概率为( )
| A. | $\frac{π}{16}$ | B. | $\frac{5}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
3.已知由不等式$\left\{{\begin{array}{l}{x≥y}\\{y≥0}\\{x+y-4≤0}\end{array}}\right.$所确定的平面区域为M,由不等式x2+y2≤8所确定的平面区域为N,区域M内随机抽取一个点,该点同时落在区域N内的概率是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{16}$ | D. | $\frac{π}{4}$ |
3.已知集合A={x|(x-1)(3-x)<0},B={x|-2≤x≤2},则A∩B=( )
| A. | [-2,1) | B. | (1,2] | C. | [-2,-1) | D. | (-1,2] |
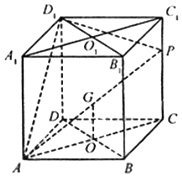 如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m