题目内容
已知函数f(x)=ln x+mx2(m∈R).
(1)求函数f(x)的单调区间;
(2)若A,B是函数f(x)图像上不同的两点,且直线AB的斜率恒大于1,求实数m的取值范围.
解:(1)f(x)的定义域为(0,+∞),
f′(x)=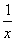 +2mx=
+2mx=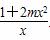 .
.
当m≥0时,f′(x)>0,f(x)在(0,+∞)上单调递增.
当m<0时,由f′(x)=0得x=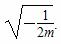 .
.
当x∈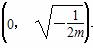 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在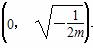 上单调递增;
上单调递增;
当x∈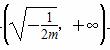 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在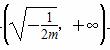 上单调递减.
上单调递减.
综上所述,当m≥0时,f(x)在(0,+∞)上单调递增;
当m<0时,f(x)在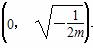 上单调递增,在
上单调递增,在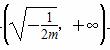 上单调递减.
上单调递减.
(2)依题意,设A(a,f(a)),B(b,f(b)),不妨设a>b>0,
则kAB=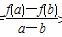 >1恒成立,
>1恒成立,
即f(a)-f(b)>a-b恒成立,
即f(a)-a>f(b)-b恒成立,
令g(x)=f(x)-x=ln x+mx2-x,
则g(x)在(0,+∞)上为增函数,
所以g′(x)=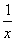 +2mx-1=
+2mx-1=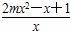 ≥0对x∈(0,+∞)恒成立,
≥0对x∈(0,+∞)恒成立,
所以2mx2-x+1≥0对x∈(0,+∞)恒成立,
即2m≥- +
+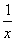 =-
=-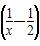 2+
2+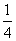 对x∈(0,+∞)恒成立,因此m≥
对x∈(0,+∞)恒成立,因此m≥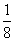 .
.
故实数m的取值范围为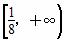 .
.

练习册系列答案
相关题目
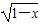 B.y=|x-2|
B.y=|x-2|

 x3-
x3- x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.
x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.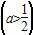 ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )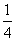 B.
B.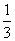
 D.1
D.1 ,则cos α=________.
,则cos α=________.