题目内容
8.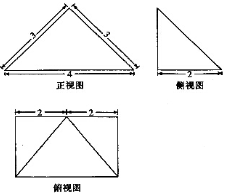 四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )| A. | $\frac{81π}{5}$ | B. | $\frac{81π}{20}$ | C. | $\frac{101π}{5}$ | D. | $\frac{101π}{20}$ |
分析 如图所示,四棱锥P-ABCD.对角线AC∩BD=F点,取AD的中点E,设此四棱锥外接球的半径为r,连接OP,OF,OA.设OF=x,则${x}^{2}+(\frac{\sqrt{{2}^{2}+{4}^{2}}}{2})^{2}$=$(\sqrt{{3}^{2}-{2}^{2}}-x)^{2}$+1,解得x即可得出.
解答 解:如图所示,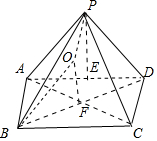 四棱锥P-ABCD.
四棱锥P-ABCD.
对角线AC∩BD=F点,取AD的中点E,设此四棱锥外接球的半径为r,连接OP,OF,OA.
设OF=x,则${x}^{2}+(\frac{\sqrt{{2}^{2}+{4}^{2}}}{2})^{2}$=$(\sqrt{{3}^{2}-{2}^{2}}-x)^{2}$+1,
解得x=$\frac{1}{2\sqrt{5}}$.
∴r=OB=$\sqrt{(\frac{1}{2\sqrt{5}})^{2}+(\sqrt{5})^{2}}$=$\sqrt{\frac{101}{20}}$.
该四棱锥的外接球的表面积=4πr2=$\frac{101π}{5}$.
故选:C.
点评 本题考查了四棱锥的三视图、球的表面积计算公式、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
18.下列函数既是奇函数又在(-1,1)上是减函数的是( )
| A. | y=tanx | B. | y=x-1 | C. | y=log${\;}_{\frac{1}{2}}$$\frac{3+x}{3-x}$ | D. | y=$\frac{1}{3}$(3x-3-x) |
16.将曲线y=sin 2x按照伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=3y}\end{array}\right.$后得到的曲线方程为( )
| A. | y=3sin x | B. | y=3sin 2x | C. | y=3sin$\frac{1}{2}$x | D. | y=$\frac{1}{3}$sin 2x |
20.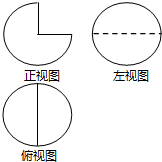 某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )
 某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图,其俯视图与左视图均为半径是$\frac{1}{2}$的圆,则该几何体的表面积是( )| A. | 16π | B. | 8π | C. | π | D. | $\frac{π}{8}$ |