若不等式|x+1|+|x-3|≥a对任意的实数x恒成立.则实数a的取值范围是(-∞.4]．题目和参考答案——青夏教育精英家教网—

题目内容

18．若不等式|x+1|+|x-3|≥a对任意的实数x恒成立，则实数a的取值范围是（-∞，4]．

分析由条件根据绝对值的意义求得|x+2|+|x-3|的最小值为5，从而得到实数a的取值范围．

解答解：由于|x+1|+|x-3|表示数轴上的x对应点到-1、3对应点的距离之和，它的最小值为4，
不等式|x+1|+|x-3|≥a对任意的实数x恒成立，故a≤4，
故答案为：（-∞，4]．

点评本题主要考查绝对值的意义，绝对值不等式的解法，函数的恒成立问题，体现了转化的数学思想，属于基础题．

练习册系列答案

浙江新课程三维目标测评课时特训系列答案

相关题目

8．

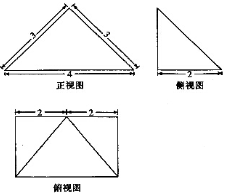四棱锥P-ABCD的三视图如图所示，则该四棱锥的外接球的表面积为（　　）

9．在△ABC中，已知A=60°，$c=\sqrt{3}$，$b=2\sqrt{3}$，则a=3．

6．已知x，y满足$\left\{\begin{array}{l}y≥-1\\ x+y≤1\\ y≤x\end{array}\right.$，则z=2x+y的最小值是（　　）

13．复数${z_1}=a+5+（10-{a^2}）i$，z₂=1-2a+（2a-5）i，其中a∈R．
（1）若a=-2，求z₁的模；
（2）若$\overline{z_1}+{z_2}$是实数，求实数a的值．

3．已知全集U={1，2，3，4，5，6，7}，集合A={2，4，5}，B={1，3，5，7}，则（∁_UA）∩B={1，3，7}．

10．已知函数y=f（x）的导函数y=f′（x）的图象如图所示，则关于函数y=f（x），下列说法正确的是（　　）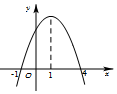

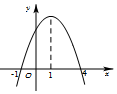
	A．	在x=-1处取得极大值		B．	在区间[-1，4]上是增函数
	C．	在x=1处取得极大值		D．	在区间[1，+∞）上是减函数

7．为了加强某站的安全检查，从甲乙丙等5名候选民警中选2名作为安保人员，则甲乙丙中有2人被选中的概率为（　　）

8．一动圆P与圆A：（x+1）²+y²=1外切，而与圆B：（x-1）²+y²=r²（r＞3或0＜r＜1）内切，那么动圆的圆心P的轨迹是（　　）

	A．	椭圆		B．	双曲线
	C．	椭圆或双曲线一支		D．	抛物线

试题分类