题目内容
16.将曲线y=sin 2x按照伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=3y}\end{array}\right.$后得到的曲线方程为( )| A. | y=3sin x | B. | y=3sin 2x | C. | y=3sin$\frac{1}{2}$x | D. | y=$\frac{1}{3}$sin 2x |
分析 利用代入法,即可得到伸缩变换的曲线方程.
解答 解:∵伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=3y}\end{array}\right.$,
∴x=$\frac{1}{2}$x′,y=$\frac{1}{3}$y′,
代入曲线y=sin2x可得y′=3sin x′,即y=3sin x.
故选A.
点评 本题考查代入法求轨迹方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
8.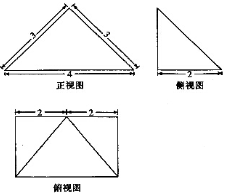 四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
 四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )| A. | $\frac{81π}{5}$ | B. | $\frac{81π}{20}$ | C. | $\frac{101π}{5}$ | D. | $\frac{101π}{20}$ |
6.已知x,y满足$\left\{\begin{array}{l}y≥-1\\ x+y≤1\\ y≤x\end{array}\right.$,则z=2x+y的最小值是( )
| A. | -3 | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |