题目内容
17.已知公差不为0的等差数列{an}的首项a1为1,前n项和为Sn,且a1,a2,a4成等比数列,则$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{{{S_{15}}}}$=$\frac{15}{8}$.分析 利用等差数列通项公式和a1,a2,a4成等比数列,求出d=1,从而$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=$\frac{1}{2}$($\frac{1}{n}-\frac{1}{n+1}$),由此利用裂项求和法能求出$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{{{S_{15}}}}$的值.
解答 解:∵公差不为0的等差数列{an}的首项a1为1,前n项和为Sn,
且a1,a2,a4成等比数列,
∴${{(a}_{1}+d)}^{2}={a}_{1}({a}_{1}+3d)$,
即(1+d)2=1+3d,
解得d=1或d=0(舍),
∴Sn=$n+\frac{n(n-1)}{2}×1$=$\frac{{n}^{2}+n}{2}$,
∴$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=$\frac{1}{2}$($\frac{1}{n}-\frac{1}{n+1}$),
∴$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{{{S_{15}}}}$=$\frac{1}{2}$(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{15}-\frac{1}{16}$)=$\frac{15}{8}$.
故答案为:$\frac{15}{8}$.
点评 本题考查等差数列中前n项和的倒数的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
8.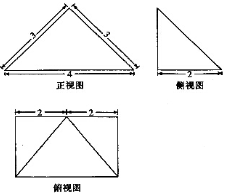 四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
 四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )| A. | $\frac{81π}{5}$ | B. | $\frac{81π}{20}$ | C. | $\frac{101π}{5}$ | D. | $\frac{101π}{20}$ |
12.已知不等式x2+ax+b<0的解集是{x|-1<x<2},则a+b等于( )
| A. | -3 | B. | 1 | C. | -1 | D. | 3 |
6.已知x,y满足$\left\{\begin{array}{l}y≥-1\\ x+y≤1\\ y≤x\end{array}\right.$,则z=2x+y的最小值是( )
| A. | -3 | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
7.为了加强某站的安全检查,从甲乙丙等5名候选民警中选2名作为安保人员,则甲乙丙中有2人被选中的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |