题目内容
19.三角形ABC的角A.B.C的对边分别为a.b.c.已知10acosB=3bcosA,$cosA=\frac{{5\sqrt{26}}}{26}$,则C=$\frac{3π}{4}$.分析 $cosA=\frac{{5\sqrt{26}}}{26}$,A∈(0,π),可得sinA=$\sqrt{1-co{s}^{2}A}$.由10acosB=3bcosA,利用正弦定理可得:10sinAcosB=3sinBcosA,可得2cosB=3sinB,与sin2B+cos2B=1联立解得:cosB(>0),sinB.再利用cosC=-cos(A+B)=sinAsinB-cosAcosB即可得出.
解答 解:∵$cosA=\frac{{5\sqrt{26}}}{26}$,A∈(0,π),∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{1}{\sqrt{26}}$.
∵10acosB=3bcosA,∴10sinAcosB=3sinBcosA,
∴10×$\frac{1}{\sqrt{26}}$cosB=3sinB×$\frac{5\sqrt{26}}{26}$,
∴2cosB=3sinB,
又sin2B+cos2B=1.
联立解得:cosB=±$\frac{3}{\sqrt{13}}$,sinB=$\frac{2}{\sqrt{13}}$.
取cosB=$\frac{3}{\sqrt{13}}$,
则cosC=-cos(A+B)=sinAsinB-cosAcosB=$\frac{1}{\sqrt{26}}$×$\frac{2}{\sqrt{13}}$-$\frac{5\sqrt{26}}{26}$×$\frac{3}{\sqrt{13}}$=$-\frac{\sqrt{2}}{2}$.
C∈(0,π).
∴C=$\frac{3π}{4}$.
故答案为:$\frac{3π}{4}$.
点评 本题考查了正弦定理余弦定理的应用、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
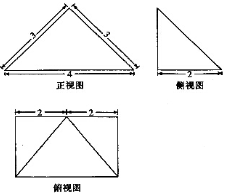 四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )
四棱锥P-ABCD的三视图如图所示,则该四棱锥的外接球的表面积为( )| A. | $\frac{81π}{5}$ | B. | $\frac{81π}{20}$ | C. | $\frac{101π}{5}$ | D. | $\frac{101π}{20}$ |