题目内容
20．
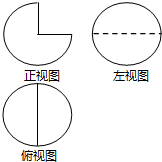某几何体的三视图如图，其俯视图与左视图均为半径是$\frac{1}{2}$的圆，则该几何体的表面积是（ ）| A． | 16π | B． | 8π | C． | π | D． | $\frac{π}{8}$ |
分析 该几何体是由一个球去掉$\frac{1}{4}$．利用球与圆的表面积计算公式即可得出．
解答 解：由三视图可知：该几何体是由一个球去掉$\frac{1}{4}$．
∴该几何体的表面积=$\frac{3}{4}×4π（\frac{1}{2}）^{2}$+$π×（\frac{1}{2}）^{2}$=π．
故选：C．
点评 本题考查了球的三视图与表面积计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
8．
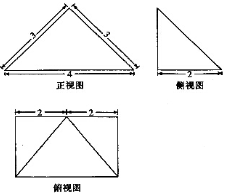四棱锥P-ABCD的三视图如图所示，则该四棱锥的外接球的表面积为（ ）
四棱锥P-ABCD的三视图如图所示，则该四棱锥的外接球的表面积为（ ）| A． | $\frac{81π}{5}$ | B． | $\frac{81π}{20}$ | C． | $\frac{101π}{5}$ | D． | $\frac{101π}{20}$ |
12．已知不等式x2+ax+b＜0的解集是{x|-1＜x＜2}，则a+b等于（ ）
| A． | -3 | B． | 1 | C． | -1 | D． | 3 |
10．已知函数y=f（x）的导函数y=f′（x）的图象如图所示，则关于函数y=f（x），下列说法正确的是（ ）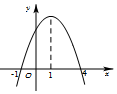
| A． | 在x=-1处取得极大值 | B． | 在区间[-1，4]上是增函数 | ||
| C． | 在x=1处取得极大值 | D． | 在区间[1，+∞）上是减函数 |