题目内容
在锐角△ABC中,AC=BC=2,
=x
+y
,(其中x+y=1),函数f(λ)=|
-λ
|的最小值为
,则|
|的最小值为 .
| CO |
| CA |
| CB |
| CA |
| CB |
| 3 |
| CO |
考点:平面向量数量积的运算
专题:函数的性质及应用,平面向量及应用
分析:由题意,利用数量积求模长得出∠ACB的大小,再利用数量积和二次函数的性质求出|
|的最小值.
| CO |
解答:
解:锐角△ABC中,AC=BC=2,且函数f(λ )的最小值为
;
∴函数f(λ)=
=2
≥
,
即4λ2-8λcos∠ACB+1≥0恒成立;
当且仅当λ=-
=cos∠ACB时等号成立,
代入函数f(λ)中得到cos∠ACB=
,
∴∠ACB=
;
∴|
|=
=2
=2
=2
=2
≥2×
=
,
当且仅当x=
=y时,取得最小值
,
∴|
|的最小值为
;
故答案为:
.
| 3 |
∴函数f(λ)=
|
=2
| 1+λ2-2λcos∠ACB |
| 3 |
即4λ2-8λcos∠ACB+1≥0恒成立;
当且仅当λ=-
| -8cos∠ACB |
| 2×4 |
代入函数f(λ)中得到cos∠ACB=
| 1 |
| 2 |
∴∠ACB=
| π |
| 3 |
∴|
| CO |
(x
|
=2
| x2+2xycos∠ACB+y2 |
=2
x2+2x(1-x)×
|
=2
| x2-x+1 |
=2
(x-
|
|
| 3 |
当且仅当x=
| 1 |
| 2 |
| 3 |
∴|
| CO |
| 3 |
故答案为:
| 3 |
点评:本题考查了平面向量的数量积的应用以及一元二次不等式与二次函数的最值问题,是综合题目.

练习册系列答案
相关题目
已知i是虚数单位,若复数z满足i=
,则z=( )
| 1-i |
| z |
| A、-1-i | B、-1+i |
| C、1-i | D、1+i |
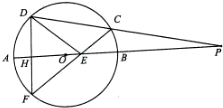 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.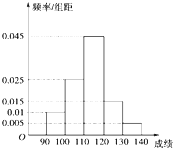 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.