题目内容
12.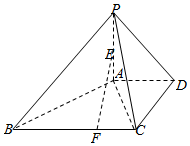 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.(Ⅰ)证明:EF∥平面PCD;
(Ⅱ)证明:平面PAB⊥平面PAC.
分析 (I)取PD的中点M,连结EM,CM,证明四边形EFCM是平行四边形可得EF∥CM,故而EF∥平面PCD;
(II)取BC的中点N,连结AN,则可证明AB⊥AC,结合AC⊥PA即可得出AC⊥平面PAB,于是平面PAB⊥平面PAC.
解答 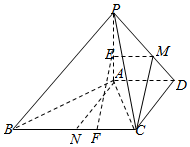 证明:(I)取PD的中点M,连结EM,CM,
证明:(I)取PD的中点M,连结EM,CM,
∵E,M分别是PA,PD的中点,
∴EM$\stackrel{∥}{=}$$\frac{1}{2}$AD,又CF$\stackrel{∥}{=}$$\frac{1}{2}$AD,
∴四边形EFCM是平行四边形,
∴EF∥CM,又EF?平面PCD,CM?平面PCD,
∴EF∥平面PCD.
(II)取BC的中点N,连结AN,则CN=BN=AN=2,
∴△ABN和△ACN均为等腰直角三角形,
∴∠BAN=∠CAN=45°,∴AB⊥AC,
∵PA⊥平面ABCD,AC?平面ABCD,
∴AC⊥PA,
又PA?平面PAB,AB?平面PAB,PA∩AB=A,
∴AC⊥平面PAB,又AC?平面PAC,
∴平面PAB⊥平面PAC.
点评 本题考查了线面平行的判定,面面垂直的判定,属于中档题.

练习册系列答案
相关题目
2.复数z满足$({1-\sqrt{3}i})z=i$(S为虚数单位),则|z|=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
3.已知数列{an}为等比数列,若a2=2,a10=8,则a6=( )
| A. | ±4 | B. | -4 | C. | 4 | D. | 5 |
7.若函数f(x)满足:当x<1时,f(x)=($\frac{1}{2}$)x;当x≥1时,f(x+1)=-f(x),则f(2017+log23)=( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
4.已知sinθ=-$\frac{3}{4}$且θ为第四象限角,则tan(π-θ)=( )
| A. | -$\frac{3\sqrt{7}}{7}$ | B. | $\frac{3\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{3}$ | D. | -$\frac{\sqrt{7}}{3}$ |