题目内容
20.给出下列四个结论:①${∫}_{-a}^{a}$(x2+sinx)dx=18,则a=3;
②用相关指数R2来刻画回归效果,R2的值越大,说明模型的拟合效果越差;
③若f(x)是定义在R上的奇函数,且满足f(x+2)=-f(x),则函数f(x)的图象关于x=1对称;
④已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ<-2)=0.21;
其中正确结论的序号为①③④.
分析 求出被积函数,由定积分公式,计算可得a,即可判断①;
由用相关指数R2来刻画回归效果,R2的值越大,说明模型的拟合效果越好,即可判断②;
应用奇函数的定义和对称性,即可判断③;
由正态分布的特点,曲线关于x=1对称,即可判断④.
解答 解:对于①,${∫}_{-a}^{a}$(x2+sinx)dx=($\frac{1}{3}$x3-cosx)|${\;}_{-a}^{a}$=$\frac{2}{3}$a3-0=18,则a=3,故正确;
对于②,用相关指数R2来刻画回归效果,R2的值越大,说明模型的拟合效果越好,故错误;
对于③,若f(x)是定义在R上的奇函数,可得f(-x)=-f(x),又f(x+2)=-f(x),即有f(2+x)=f(-x),
则函数f(x)的图象关于x=1对称,故正确;
对于④,已知随机变量ξ服从正态分布N(1,σ2),曲线关于x=1对称,P(ξ≤4)=0.79,
则P(ξ<-2)=P(ξ>4)=1-P(ξ≤4)=1-0.79=0.21,故正确.
故答案为:①③④.
点评 本题考查命题的真假判断和应用,考查定积分的计算和线性回归的特点,以及函数的对称性和正态分布的特点,考查判断能力和运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则f(5)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
8.为了解某班学生喜欢打篮球是否与性别有关,对本班50人进行了问卷调查,得到如下2×2列联表:
经计算得到随机变量K2的观测值为8.333,则有99.5%的把握认为喜爱打篮球与性别有关(临界值参考表如下).
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥K0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9.已知集合A={x|(x-1)(x-4)≤0},$B=\{x|\frac{x-5}{x-2}≤0\}$,则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|1≤x<2} | C. | {x|2≤x≤4} | D. | {x|2<x≤4} |
10.2016年济南地铁正式开工建设,地铁时代的到来能否缓解济南的交通拥堵状况呢?某社团进行社会调查,得到的数据如表:
则下列结论正确的是( )
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| 男性市民 | 女性市民 | |
| 认为能缓解交通拥堵 | 48 | 30 |
| 认为不能缓解交通拥堵 | 12 | 20 |
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| B. | 有95%的把握认为“对能否缓解交通拥堵的认识与性别无关” | |
| C. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别有关” | |
| D. | 有99%的把握认为“对能否缓解交通拥堵的认识与性别无关” |
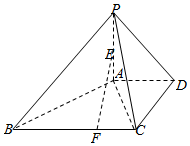 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.