题目内容
7.若函数f(x)满足:当x<1时,f(x)=($\frac{1}{2}$)x;当x≥1时,f(x+1)=-f(x),则f(2017+log23)=( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
分析 求出x≥1时,函数的周期,化简所求的表达式,通过x<1时,f(x)=($\frac{1}{2}$)x;求解即可.
解答 解:函数f(x)满足:当x<1时,f(x)=($\frac{1}{2}$)x;
当x≥1时,f(x+1)=-f(x),f(x+2)=-f(x+1)=f(x),可知函数的周期为:2,
则f(2017+log23)=f(1+log23)=f(log23-1)=$(\frac{1}{2})^{lo{g}_{2}3-1}$=$\frac{2}{3}$.
故选:D.
点评 本题考查抽象函数的应用,分段函数的应用,考查计算能力.

练习册系列答案
相关题目
18.集合A={2,4,6,8,10},B={1,3,5,7,9},在A中任取一元素m和在B中任取一元素n,则所取两数m>n的概率是( )
| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.7 |
2.复数z=$\frac{2-i}{1-2i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.复数$z=\frac{{({1-i})({4-i})}}{1+i}$的共轭复数是( )
| A. | -4i | B. | -4 | C. | 4i | D. | -1+4i |
16.设G是△ABC的重心,点E是AG的中点,若$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BG}$•$\overrightarrow{CG}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
| A. | -$\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{13}{8}$ |
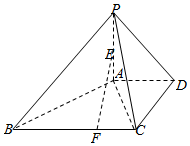 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,BC=4,AD=DC=2,E为PA的中点,F为线段BC上一点,且CF=1.