题目内容
当x∈[0,
]时,讨论关于x的方程2cos2x-sinx+α=0(α∈R)实根的个数.
| 7π |
| 6 |
考点:根的存在性及根的个数判断,同角三角函数基本关系的运用
专题:函数的性质及应用
分析:令t=sinx(0≤x≤
),a=2(t+
)2-
,t∈[-
,1],作出函数的图象,通过讨论a的范围,得出方程的根的个数.
| 7π |
| 6 |
| 1 |
| 4 |
| 17 |
| 8 |
| 1 |
| 2 |
解答:
解:有方程2cos2x-sinx+a=0可得a=-2cos2x+sinx,
∴a=2sin2x+sinx-2,
a=2(sinx+
)2-
,
∵0≤x≤
,∴-
≤sinx≤1,
-
≤2(sinx+
)2-
≤1,
令t=sinx(0≤x≤
),
∴a=2(t+
)2-
,t∈[-
,1],
画出函数图象,如图示:
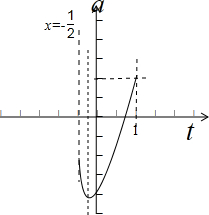
(1)当a≤-
或a>1时,方程没有实数根;
(2)当a=-2时,得sinx=
或0,可得x=0或x=
,即方程有3个实数根;
(3)当a=1时,得sinx=
或1,可得x=
,即方程有1个实数根;
(4)当-
<a<-2或-2<a<1时,每一个a值都对应两个不同的x值,即方程有2个实数根.
∴a=2sin2x+sinx-2,
a=2(sinx+
| 1 |
| 4 |
| 17 |
| 8 |
∵0≤x≤
| 7π |
| 6 |
| 1 |
| 2 |
-
| 17 |
| 8 |
| 1 |
| 4 |
| 17 |
| 8 |
令t=sinx(0≤x≤
| 7π |
| 6 |
∴a=2(t+
| 1 |
| 4 |
| 17 |
| 8 |
| 1 |
| 2 |
画出函数图象,如图示:
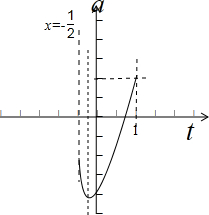
(1)当a≤-
| 17 |
| 8 |
(2)当a=-2时,得sinx=
| 1 |
| 2 |
| 7π |
| 6 |
(3)当a=1时,得sinx=
| 3 |
| 2 |
| π |
| 2 |
(4)当-
| 17 |
| 8 |
点评:本题考查了方程根的存在性,考查了三角函数问题,本题属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
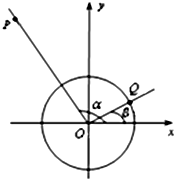 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为