题目内容
已知函数f（x）=sinx+acosx的图象经过点（-
，0）．
（1）求实数a的值；
（2）设g（x）=[f（x）]2-2，求函数g（x）的最小正周期与单调递增区间．
| π |
| 3 |
（1）求实数a的值；
（2）设g（x）=[f（x）]2-2，求函数g（x）的最小正周期与单调递增区间．
考点：函数y=Asin（ωx+φ）的图象变换,三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：函数的性质及应用
分析：（1）根据函数f（x）的图象经过点(-
，0)，可得sin(-
)+acos(-
)=0，由此求得a的值．
（2）由（1）得f(x)=sinx+
cosx，利用三角恒等变换化简g（x）=[f（x）]2-2的解析式为2sin(2x+
)，可得函数的最小正周期．令2kπ-
≤2x+
≤2kπ+
，k∈z，求得x的范围，可得函数的增区间．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
（2）由（1）得f(x)=sinx+
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解答：
解：（1）∵函数f（x）=sinx+acosx的图象经过点(-
，0)，∴f(-
)=0，
即sin(-
)+acos(-
)=0，即-
+
=0，解得a=
．
（2）由（1）得f(x)=sinx+
cosx．
∴g（x）=[f（x）]2-2=(sinx+
cosx)2-2=sin2x+2
sinxcosx+3cos2x-2=
sin2x+cos2x
=2(
sin2x+
cos2x)=2(sin2xcos
+cos2xsin
)=2sin(2x+
)．
∴函数的最小正周期为
=π．
∵函数y=sinx的单调递增区间为[2kπ-
，2kπ+
]（k∈Z），
令2kπ-
≤2x+
≤2kπ+
，k∈z，求得 kπ-
≤x≤kπ+
，
∴函数的单调递增区间为[kπ-
，kπ+
]（k∈Z）．
| π |
| 3 |
| π |
| 3 |
即sin(-
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| a |
| 2 |
| 3 |
（2）由（1）得f(x)=sinx+
| 3 |
∴g（x）=[f（x）]2-2=(sinx+
| 3 |
| 3 |
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴函数的最小正周期为
| 2π |
| 2 |
∵函数y=sinx的单调递增区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
点评：本题主要考查三角函数图象的周期性、单调性、同角三角函数的基本关系和三角函数倍角公式等等知识，考查化归与转化的数学思想方法，以及运算求解能力，属于中档题．
练习册系列答案
相关题目
函数f（x）=sin2x-sin（2x+
）的最小值为（ ）
| π |
| 3 |
| A、0 | ||
| B、-1 | ||
C、-
| ||
| D、-2 |
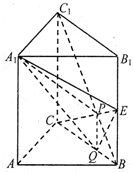如图在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AA1=2，E是BB1的中点，且CE交BC1于点P，点Q在线段BC上，CQ=2QB．
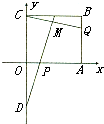如图所示，在直角坐标平面上的矩形OABC中，|OA|=2，|OC|=