题目内容
2008年5月12日,四川汶川发生8.0级特大地震,通往灾区的道路全部中断.5月12日晚,抗震救灾指挥部决定从水路(一支队伍)、陆路(东南和西北两个方向各一支队伍)和空中(一支队伍)同时向灾区挺进.在5月13日,仍时有较强余震发生,天气状况也不利于空中航行.已知当天从水路抵达灾区的概率是
,从陆路每个方向抵达灾区的概率都是
,从空中抵达灾区的概率是
.
(Ⅰ)求在5月13日恰有1支队伍抵达灾区的概率;
(Ⅱ)求在5月13日抵达灾区的队伍数ξ的数学期望.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(Ⅰ)求在5月13日恰有1支队伍抵达灾区的概率;
(Ⅱ)求在5月13日抵达灾区的队伍数ξ的数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)由相互独立事件的概率乘法公式能求出在5月13日恰有1支队伍抵达灾区的概率.
(Ⅱ)设5月13日抵达灾区的队伍数为ξ,则ξ=0、1、2、3、4.分别求出P(ξ=0),P(ξ=1),P(ξ=2),
P(ξ=3),P(ξ=4),由此能求出在5月13日抵达灾区的队伍数ξ的数学期望.
(Ⅱ)设5月13日抵达灾区的队伍数为ξ,则ξ=0、1、2、3、4.分别求出P(ξ=0),P(ξ=1),P(ξ=2),
P(ξ=3),P(ξ=4),由此能求出在5月13日抵达灾区的队伍数ξ的数学期望.
解答:
(理)(Ⅰ)解:依据题意,∵队伍从水路或陆路抵达灾区的概率相等,
将“队伍从水路或陆路抵达灾区”视为同一个事件.
记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,
而且P(B)=
,P(C)=
.…(2分)
在5月13日恰有1支队伍抵达灾区的概率是
P(ξ=1)=
×
×(1-
)2
×(1-
)3×
=
.…(5分)
(Ⅱ)解:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,
则将“队伍从水路或陆路抵达灾区”视为同一个事件.
记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,
而且P(B)=
,P(C)=
.
设5月13日抵达灾区的队伍数为ξ,则ξ=0、1、2、3、4.…(6分)
由已知有:P(ξ=0)=
×(1-
)3×
=
,…(7分)
P(ξ=1)=
×
×(1-
)2
×(1-
)3×
=
,…(8分)
P(ξ=2)=
(
)2(1-
)×
+
×
×(1-
)2×
=
,…(9分)
P(ξ=3)=
×(
)3×
+
×(
)2+(1-
)×
=
,…(10分)
P(ξ=4)=
×(
)3×
=
.…(10分)
因此其概率分布为:
…(11分)
所以在5月13日抵达灾区的队伍数ξ的数学期望为:
Eξ=0×
+1×
+2×
+3×
+4×
=
.…(12分)
将“队伍从水路或陆路抵达灾区”视为同一个事件.
记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,
而且P(B)=
| 1 |
| 4 |
| 1 |
| 2 |
在5月13日恰有1支队伍抵达灾区的概率是
P(ξ=1)=
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| +C | 0 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 16 |
(Ⅱ)解:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,
则将“队伍从水路或陆路抵达灾区”视为同一个事件.
记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,
而且P(B)=
| 1 |
| 4 |
| 1 |
| 2 |
设5月13日抵达灾区的队伍数为ξ,则ξ=0、1、2、3、4.…(6分)
由已知有:P(ξ=0)=
| C | 0 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 32 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| +C | 0 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 16 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 8 |
P(ξ=3)=
| C | 3 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 16 |
P(ξ=4)=
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
因此其概率分布为:
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
所以在5月13日抵达灾区的队伍数ξ的数学期望为:
Eξ=0×
| 3 |
| 32 |
| 5 |
| 16 |
| 3 |
| 8 |
| 3 |
| 16 |
| 1 |
| 32 |
| 7 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的数学期的求法,解题时要认真审题,注意相互独立事件的概率乘法公式的合理运用.

练习册系列答案
相关题目
直线y=x+2与曲线
-
=1的交点个数为( )
| y2 |
| 2 |
| x|x| |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点. 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍所对应的变换矩阵. 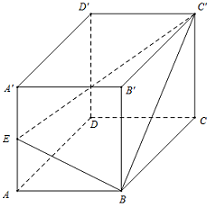 已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值.
已知正方体ABCD-A′B′C′D′中,E是AA′棱的中点.求平面BEC′与平面ABCD所成的角的余弦值. 如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.
如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.