题目内容
13.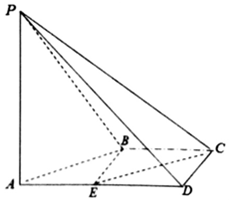 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°. (Ⅰ)证明:△PBE是直角三角形;
(Ⅱ)若二面角P-CD-A的大小为45°,求二面角A-PE-C的余弦值.
分析 (Ⅰ)由已知证明PA⊥平面ABCD,得PA⊥BE.再由已知证明四边形BCDE为平行四边形,得BE∥CD.结合CD⊥AD,得BE⊥AD.再由线面垂直的判定得BE⊥平面PAD,进一步得到BE⊥PE,得到△PBE是直角三角形;
(Ⅱ)由(Ⅰ)知,CD⊥平面PAD,则∠PDA为二面角P-CD-A的平面角为45°,设BC=1,得AD=PA=2.在平面ABCD中,过A作Ay⊥AD.以A为原点,分别以AD、Ay、AP所在直线为x、y、z轴建立空间直角坐标系.求得E,P,C的坐标,求出平面PEC与平面PAE的一个法向量,由两法向量所成角的余弦值可得二面角A-PE-C的余弦值.
解答 (Ⅰ)证明:如图,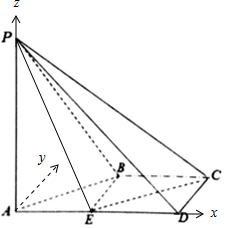
∵AD∥BC,AD=2BC,∴四边形ABCD为梯形,则AB与DC相交.
∵∠PAB=90°,∴PA⊥AB,
又异面直线AP与CD所成的角为90°,∴PA⊥CD.
∴PA⊥平面ABCD,则PA⊥BE.
∵AD∥BC,BC=$\frac{1}{2}AD=ED$,
∴四边形BCDE为平行四边形,则BE∥CD.
∵∠ADC=90°,∴CD⊥AD,
∴BE⊥AD.
由BE⊥PA,BE⊥AD,PA∩AD=A,得BE⊥平面PAD,
∴BE⊥PE,则△PBE是直角三角形;
(Ⅱ)解:由(Ⅰ)知,CD⊥平面PAD,则∠PDA为二面角P-CD-A的平面角为45°,
设BC=1,则AD=PA=2.
在平面ABCD中,过A作Ay⊥AD.
以A为原点,分别以AD、Ay、AP所在直线为x、y、z轴建立空间直角坐标系.
则E(1,0,0),P(0,0,2),C(2,1,0).
$\overrightarrow{EC}=(1,1,0),\overrightarrow{EP}=(-1,0,2)$.
设平面PEC的一个法向量为$\overrightarrow{n}=(x,y,z)$.
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=0}\\{\overrightarrow{n}•\overrightarrow{EP}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x+y=0}\\{-x+2z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}=(2,-2,1)$.
由图可知,平面PAE的一个法向量为$\overrightarrow{m}=(0,1,0)$.
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{-2}{1×3}=-\frac{2}{3}$.
∴二面角A-PE-C的余弦值为$-\frac{2}{3}$.
点评 本题考查直线与平面垂直的判定,考查面面垂直的性质,考查空间想象能力和思维能力,训练了利用空间向量求二面角的平面角,是中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案| A. | 20 | B. | 120 | C. | 2400 | D. | 14400 |
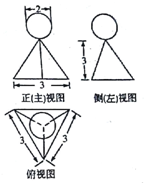 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4π}{3}$+$\frac{9\sqrt{3}}{4}$ | B. | $\frac{4π}{3}$+$\frac{27\sqrt{3}}{4}$ | C. | $\frac{8π}{3}$+$\frac{9\sqrt{3}}{4}$ | D. | $\frac{8π}{3}$+$\frac{27\sqrt{3}}{4}$ |
| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
| A. | $\frac{\sqrt{82}}{2}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 5 |
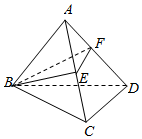 如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.
如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.