题目内容
5.已知f(x)=|x-1|+|x+1|.(1)求f(x)≤x+2的解集;
(2)若$g(x)=|{x+\frac{3}{2}}|+|{x-\frac{3}{2}}|(x∈$R),求证:$\frac{{|{a+1}|-|{2a-1}|}}{|a|}≤g(x)$对?a∈R,且a≠0成立.
分析 (1)讨论x的范围,去掉绝对值符号解出;
(2)利用绝对值不等式的性质转化得出.
解答 解:(1)当x≤-1时,不等式f(x)≤x+2为:1-x-x-1≤x+2,解得x≥-$\frac{2}{3}$(舍);
当-1<x≤1时,不等式f(x)≤x+2为:1-x+x+1≤x+2,解得x≥0,∴0≤x≤1;
当x>1时,不等式f(x)≤x+2为:x-1+x+1≤x+2,解得x≤2,∴1<x≤2.
综上,f(x)≤x+2的解集为{x|0≤x≤2}.
(2)∵g(x)=|x+$\frac{3}{2}$|+|x-$\frac{3}{2}$|≥|x+$\frac{3}{2}$-x+$\frac{3}{2}$|=3,
而$\frac{|a+1|-|2a-1|}{|a|}$≤$|{\frac{{|{a+1}|-|{2a-1}|}}{|a|}}|=|{|{1+\frac{1}{a}}|-|{2-\frac{1}{a}}|}|$≤|1+$\frac{1}{a}$+2-$\frac{1}{a}$|=3,
∴$\frac{{|{a+1}|-|{2a-1}|}}{|a|}≤g(x)$对?a∈R,且a≠0成立.
点评 本题考查了绝对值不等式的性质与解法,属于中档题.

练习册系列答案
相关题目
16.设实数x,y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$,则z=$\frac{4x}{y}$+$\frac{y}{x}$的取值范围是( )
| A. | [4,$\frac{17}{2}$] | B. | [$\frac{13}{3}$,$\frac{17}{2}$] | C. | [4,$\frac{37}{3}$] | D. | [$\frac{17}{2}$,$\frac{37}{3}$] |
20.已知数列{an}的前n项和是Sn,则下列四个命题中,错误的是( )
| A. | 若数列{an}是公差为d的等差数列,则数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列 | |
| B. | 若数列{$\frac{{S}_{n}}{n}$}是公差为d的等差数列,则数列{an}是公差为2d的等差数列 | |
| C. | 若数列{an}是等差数列,则数列的奇数项,偶数项分别构成等差数列 | |
| D. | 若数列{an}的奇数项,偶数项分别构成公差相等的等差数列,则{an}是等差数列 |
14.tan40°+tan80°-$\sqrt{3}$tan40°tan80°的值是( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
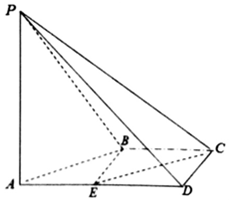 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°. 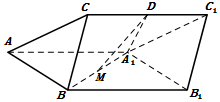 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.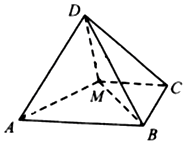 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.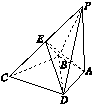 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.