题目内容
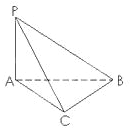
如图，在三棱锥P-ABC．中，PA⊥底面ABC．AC⊥BC，AC=BC=PA=2．求三棱锥P-ABC的体积V．
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：由已知得S△ABC=
×2×2=2，从布三棱锥P-ABC的体积V=
×PA×S△ABC，由此能求出结果．
| 1 |
| 2 |
| 1 |
| 3 |
解答：
解：∵在三棱锥P-ABC中，PA⊥底面ABC，
AC⊥BC，AC=BC=PA=2，
∴S△ABC=
×2×2=2，
∴三棱锥P-ABC的体积：V=
×PA×S△ABC=
×2×2=
．
AC⊥BC，AC=BC=PA=2，
∴S△ABC=
| 1 |
| 2 |
∴三棱锥P-ABC的体积：V=
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
点评：本题考查三棱锥的体积的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
函数f（x）=ex-x的单调递增区间是（ ）
| A、（-∞，0） |
| B、（-∞，1） |
| C、（0，+∞） |
| D、（0，1）7 q |
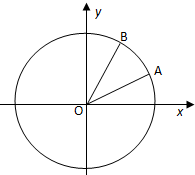如图，在平面直角坐标系xOy中，以Ox轴为始边，两个锐角α，β的终边分别与单位圆相交于A，B 两点．
某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．