Question

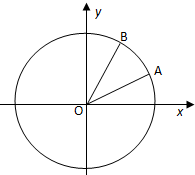如图，在平面直角坐标系xOy中，以Ox轴为始边，两个锐角α，β的终边分别与单位圆相交于A，B 两点．
（Ⅰ）若tanα=

1

7

，sinβ=

10

10

，求α+2β的值；
（Ⅱ）若角α+β的终边与单位圆交于C点，设角α，β，α+β的正弦线分别为

MA

，

NB

，

PC

，试问：以|

MA

|，|

NB

|，|

PC

|作为三边的长能否构成一个三角形？若能，请加以证明；若不能，请说明理由．

Answer 1

考点：两角和与差的正弦函数,平面向量的综合题

专题：三角函数的求值

分析：（Ⅰ）（法一）根据同角三角函数的基本关系和题意，分别求出cosα、sinα、cos2β、sin2β的值，再由两角和的余弦函数公式求出cos（α+2β），再由已知条件求出α+2β的范围，根据特殊角的余弦值确定角α+2β的值；
（法二）由条件和二倍角公式求出cos2β，再求出sin2β、tan2β，利用两角和正切公式求出tan（α+2β）的值，再由角α+2β的范围确定角α+2β的值；
（Ⅱ）根据三角函数线得：|

MA

|=sinα，|

NB

|=sinβ，|

PC

|=sin(α+β)，再由角的范围判断出cosα∈（0，1），cosβ∈（0，1），cos（α+β）∈（-1，1），再由两脚和的正弦公式分别判断出：任意两边之和大于第三边，即可证明结论．

解答： 解：（Ⅰ）（法一）：∵0＜α＜

π

2

，tanα=

1

7

，∴cosα=

7 2

10

，sinα=

2

10

．
又∵0＜β＜

π

2

，sinβ=

10

10

，∴0＜2β＜π，cos2β=1-2sin²β=

4

5

，sin2β=

1-cos22β

=

3

5

．
于是cos（α+2β）=cosαcos2β-sinαsin2β=

7 2

10

×

4

5

-

2

10

×

3

5

=

2

2

．
由已知条件知0＜α+2β＜

3

2

π，∴α+2β=

π

4

．…（6分）
（法二）：由0＜2β＜π，cos2β=1-2sin²β=

4

5

，可得出2β∈(0，

π

2

)，sin2β=

3

5

，则tan2β=

3

4

，
所以tan(α+2β)=

tanα+tan2β

1-tanαtan2β

=1，
又α+2β∈（0，π），故α+2β=

π

4

…（6分）
（Ⅱ）解：以|

MA

|，|

NB

|，|

PC

|作为三边的长能构成一个三角形，证明如下：
∵α，β∈(0，

π

2

)，∴α+β∈（0，π）
∴|

MA

|=sinα，|

NB

|=sinβ，|

PC

|=sin(α+β)
∵α，β∈(0，

π

2

)，所以cosα∈（0，1），cosβ∈（0，1），
于是有：sin（α+β）=sinαcosβ+cosαsinβ＜sinα+sinβ①…（8分）
又∵α+β∈（0，π），∴cos（α+β）∈（-1，1），
于是有：sinα=sin[（α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ＜sin（α+β）+sinβ②
同理：sinβ＜sin（α+β）+sinα③
由①②③可知，以|

MA

|，|

NB

|，|

PC

|作为三边的长能构成一个三角形．…（12分）

点评：本题考查三角恒等变换公式，同角三角函数的基本关系的应用，以及利用三角函数线和角的范围证明三角形：任意两边之和大于第三边，比较综合，考查分析解决问题的能力．