题目内容
在△ABC中,角A、B、c的时边长分别为a、b、c,已知
sinB-cosB=l,且b=1.
(Ⅰ)若A=
,求c的值;
(Ⅱ)设AC边上的高为h,求h的最大值.
| 3 |
(Ⅰ)若A=
| 5π |
| 12 |
(Ⅱ)设AC边上的高为h,求h的最大值.
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)在△ABC中,由
sinB-cosB=l求得 sin(B-
)=
.根据A=
,求得 B的值,可得 C=π-A-B的值 值,再根据b=1,利用正弦定理求得c的值.
(Ⅱ)根据
•bh=
ac•sinB,求得 h=
ac.由余弦定理可得 ac≤1,从而求得h的最大值.
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 5π |
| 12 |
(Ⅱ)根据
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答:
解:(Ⅰ)在△ABC中,∵
sinB-cosB=l=2sin(B-
),∴sin(B-
)=
.
∵A=
,∴0<B<
,∴B=
,∴C=π-A-B=
.
再根据b=1,利用正弦定理可得
=
,即
=
,解得 c=
.
(Ⅱ)设AC边上的高为h,∵
•bh=
ac•sinB,∴h=
ac.
由余弦定理可得b2=1=a2+c2-2ac•cosB=a2+c2-ac≥2ac-ac=ac,
∴ac≤1,h≤
,即h的最大值为
.
| 3 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∵A=
| 5π |
| 12 |
| 7π |
| 12 |
| π |
| 3 |
| π |
| 4 |
再根据b=1,利用正弦定理可得
| c |
| sinC |
| b |
| sinB |
| c | ||||
|
| 1 | ||||
|
| ||
| 3 |
(Ⅱ)设AC边上的高为h,∵
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由余弦定理可得b2=1=a2+c2-2ac•cosB=a2+c2-ac≥2ac-ac=ac,
∴ac≤1,h≤
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查正弦定理、余弦定理的应用,两角和差的正弦公式、基本不等式,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知2log6x=1-log63,则x的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
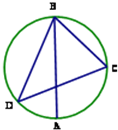 圆形广场的有南北两个大门在中轴线上,东、西各有一栋建筑物与北门的距离分别为30米和40米,且以北门为顶点(视大门和建筑物为点)的角为60°,求广场的直径(保留两位小数).
圆形广场的有南北两个大门在中轴线上,东、西各有一栋建筑物与北门的距离分别为30米和40米,且以北门为顶点(视大门和建筑物为点)的角为60°,求广场的直径(保留两位小数).