题目内容
5.函数f(x)=ax3+3x2+2,若f'(-1)=-12,则a的值等于-2.分析 先求出∴f′(x)=3ax2+6x,从而f'(-1)=3a-6=-12,由此能求出a的值.
解答 解:∵函数f(x)=ax3+3x2+2,
∴f′(x)=3ax2+6x,
∵f'(-1)=-12,
∴f'(-1)=3a-6=-12,
解得a=-2.
故答案为:-2.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
13.下列选项中,说法正确的是( )
| A. | 若命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| B. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| C. | 命题“若a=-b,则|a|=|b|”的否命题是真命题 | |
| D. | 命题“若$\left\{{\overrightarrow a,\overrightarrow b,\overrightarrow c}\right\}$为空间的一个基底,则$\left\{{\overrightarrow a+\overrightarrow b,\overrightarrow b+\overrightarrow c,\overrightarrow c+\overrightarrow a}\right\}$构成空间的另一个基底”的逆否命题为真命题 |
10.经过点A(-1,4)且在x轴上的截距为3的直线方程是( )
| A. | x+y+3=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x-y-3=0 |
14.已知等差数列{an}的前n项和为Sn,且a3+a4+a5+a6+a7=20,则S9=( )
| A. | 18 | B. | 36 | C. | 60 | D. | 72 |
15.设0<x<$\frac{π}{2}$,记a=sinx,b=esinx,c=lnsinx,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<a<b |
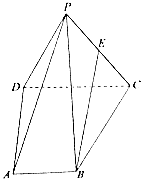 如图所示,四棱锥P-ABCD的底面为直角梯形,AB⊥AD,CD⊥AD,CD=2AB.点E是PC的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,AB⊥AD,CD⊥AD,CD=2AB.点E是PC的中点.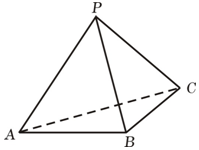 如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.
如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.