已知等差数列{an}的前n项和为Sn.且a3+a4+a5+a6+a7=20.则S9=( )A．18B．36C．60D．72 题目和参考答案——青夏教育精英家教网—

题目内容

14．已知等差数列{a_n}的前n项和为S_n，且a₃+a₄+a₅+a₆+a₇=20，则S₉=（　　）

A．

B．

C．

D．

分析由等差数列的通项公式得a₃+a₄+a₅+a₆+a₇=5a₅=20，解得a₅=4，从而S₉=$\frac{9}{2}（{a}_{1}+{a}_{9}）=9{a}_{5}$，由此能求出结果．

解答解：∵等差数列{a_n}的前n项和为S_n，且a₃+a₄+a₅+a₆+a₇=20，
∴a₃+a₄+a₅+a₆+a₇=5a₅=20，
解得a₅=4，
∴S₉=$\frac{9}{2}（{a}_{1}+{a}_{9}）=9{a}_{5}$=36．
故选：B．

点评本题考查等差数列的前9项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案

68所名校图书小学毕业升学考前突破系列答案

5．函数f（x）=ax³+3x²+2，若f'（-1）=-12，则a的值等于-2．

2．设函数f（x）=e^x-ax²+1，曲线y=f（x）在x=1处的切线方程为y=bx+2．
（1）求a，b的值；
（2）若方程F（x）=f（x）-mx有两个极值点x₁，x₂（x₁＜x₂），x₀是x₁与x₂的等差中项；
（i）求实数m的取值范围；
（ii）求证：f′（x₀）＜0 （ f′（x）为f（x）的导函数）．

9．已知向量$\overrightarrow{a}$=（1，0，1），$\overrightarrow{b}$=（0，1，1），向量$\overrightarrow{a}$-k$\overrightarrow{b}$与$\overrightarrow{a}$垂直，k为实数．
（I）求实数k的值；
（II）记$\overrightarrow{c}$=k$\overrightarrow{a}$，求向量$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{c}$-$\overrightarrow{b}$的夹角．

19．已知双曲线C的两焦点为F₁，F₂，离心率为$\frac{4}{3}$，抛物线y²=16x的准线过双曲线C的一个焦点，若以线段F₁F₂为直径的圆与双曲线交于四个点P_i（i=1，2，3，4），|P_iF₁|•|P_iF₂|=（　　）

6．执行如图所示的程序框图，输出的A值为（　　）

3．已知函数$f（x）=\left\{\begin{array}{l}{2^x}（{x≤0}）\\ \sqrt{x}（{x＞0}）\end{array}\right.$若函数g（x）=f（x）-k（x-1）有且只有一个零点，则实数k的取值范围是（　　）

14．

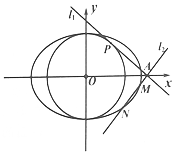已知椭圆C：$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O：x²+y²=1，过点A（m，0）（m＞1）作两条互相垂直的直线l₁，l₂，l₁于圆O相切于点P，l₂与椭圆相交于不同的两点M，N．
（1）若m=$\sqrt{2}$，求直线l₁的方程；
（2）求m的取值范围；
（3）求△OMN面积的最大值．

试题分类