题目内容
设a∈R,则“a=1”是直线“l1:ax+2y-1=0与直线l2:(a+1)x-y+4=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据直线垂直的等价条件,结合充分条件和必要条件的定义进行判断.
解答:
解:直线l1:ax+2y-1=0的斜率k1=-
,直线l2:(a+1)x-y+4=0的斜率k2=a+1,
若两直线垂直则k1k2=-
(a+1)=-1,
即a2+a-2=0,解得a=1或a=-2,
故“a=1”是直线“l1:ax+2y-1=0与直线l2:(a+1)x-y+4=0垂直”的充分不必要条件,
故选:A
| a |
| 2 |
若两直线垂直则k1k2=-
| a |
| 2 |
即a2+a-2=0,解得a=1或a=-2,
故“a=1”是直线“l1:ax+2y-1=0与直线l2:(a+1)x-y+4=0垂直”的充分不必要条件,
故选:A
点评:本题主要考查充分条件和必要条件的判断,根据直线垂直的等价条件是解决本题的关键.

练习册系列答案
相关题目
如图是某几何体的三视图,则该几何体的体积为( )
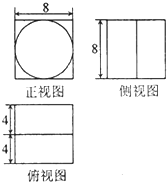

| A、256+128π |
| B、256+64π |
| C、64+64π |
| D、64+32π |
“a=2”是“直线(a2-a)x+y-1=0和2x+y+1=0互相平行”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
复数
=( )
| -i |
| 1-i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知复数z=
,i是虚数单位,则复数虚部是( )
| 1+2i |
| 3-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
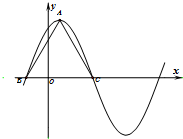 函数f(x)=6cos2
函数f(x)=6cos2