题目内容
设函数f(x)=
x-
sinx-
cosx.
(1)试判定函数f(x)的单调性,并说明理由;
(2)已知f′(x)为函数f(x)的导函数,且f′(B)=
且B为锐角,求sin(B+10°)[1-
tan(B-10°)]的值.
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 4 |
(1)试判定函数f(x)的单调性,并说明理由;
(2)已知f′(x)为函数f(x)的导函数,且f′(B)=
| 3 |
| 4 |
| 3 |
考点:利用导数研究函数的单调性,两角和与差的正弦函数
专题:导数的综合应用,三角函数的求值
分析:(1)求导,得到导数恒大于等于0,故得到函数为增函数,
(2)先求出B的大小,再利用三角函数的和差公式和诱导公式化简即可求出值.
(2)先求出B的大小,再利用三角函数的和差公式和诱导公式化简即可求出值.
解答:
解:∵f(x)=
x-
sinx-
cosx.
∴f′(x)=
-
cosx+
sinx=
sin(x-
)+
≥0,
∴函数f(x)在其定义域内单调递增.
(2)∵f′(B)=
且B为锐角,
∴
sin(B-
)+
=
,
∴sin(B-
)=
,
∴B-
=
,
∴B=60°,
∴sin(B+10°)[1-
tan(B-10°)]=sin70°(1-
tan50°)
=sin70°(1-
)=sin70°
=sin70°
=-
=-1
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 4 |
∴f′(x)=
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∴函数f(x)在其定义域内单调递增.
(2)∵f′(B)=
| 3 |
| 4 |
∴
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 4 |
∴sin(B-
| π |
| 6 |
| 1 |
| 2 |
∴B-
| π |
| 6 |
| π |
| 6 |
∴B=60°,
∴sin(B+10°)[1-
| 3 |
| 3 |
=sin70°(1-
| ||
| cos50° |
cos50°-
| ||
| cos50° |
| 2cos110° |
| cos50° |
| sin140° |
| cos50° |
点评:本题主要考查了导数与函数单调性的关系以及三角函数中的和差公式,诱导公式,培养科学生的计算能力,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
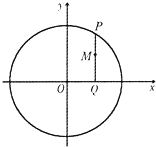 如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a
如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a