��Ŀ����
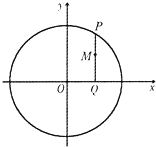 ��ͼ����P��ԲO��x2+y2=a2�ϵ�����һ�㣬����P��x�ᴹֱ��ֱ����x�ύ�ڵ�Q����M����a
��ͼ����P��ԲO��x2+y2=a2�ϵ�����һ�㣬����P��x�ᴹֱ��ֱ����x�ύ�ڵ�Q����M����a| QM |
| QP |
��1��������C�ķ��̣���ָ������CΪ����Բ���ߣ�
��2����S��m��n��ΪԲO������һ�㣬����ֱ��mx+ny=1�����еĶ�Բ�ķ��̣�
��3����S��m��n��Ϊ����C�ϵ�����һ�㣬��A��1��
| 3 |
| 2 |
���㣺�켣����,ֱ����Բ��λ�ù�ϵ
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1�����M��x��y����P��x0��y0������Q��x0��0������a
=b
����a��b��0������a��x-x0��y��=b��0��y0������P��x0��y0����Բ������һ�㣬�Ӷ�x02+y02=a2���ɴ����������C�ķ��̣�
��2���ɶԳ��ԣ�������Բ����Ϊx2+y2=r2��r��0����Բ��O��ֱ��l�ľ����r=
���ɴ��������ֱ��mx+ny=1�����еĶ�Բ�ķ��̣�
��3������֪������д����ֱ��mx+ny=1�����еĶ����ߵķ��̣�
| QM |
| QP |
��2���ɶԳ��ԣ�������Բ����Ϊx2+y2=r2��r��0����Բ��O��ֱ��l�ľ����r=
| 1 | ||
|
��3������֪������д����ֱ��mx+ny=1�����еĶ����ߵķ��̣�
���
�⣺��1�����M��x��y����P��x0��y0������Q��x0��0����
��a
=b
����a��b��0������a��x-x0��y��=b��0��y0����
��
��
��P��x0��y0����Բ������һ�㣬
��x02+y02=a2��
��x2+��
y��2=a2���������ã�
+
=1����a��b��0����
������C�ķ���Ϊ
+
=1����a��b��0����
��������������ԭ�㣬������x���ϣ����᳤Ϊ2a�����᳤Ϊ2b����Բ��
��2���ɶԳ��ԣ�������Բ����Ϊx2+y2=r2��r��0��
�����⣬��Բ��O��ֱ��l�ľ���d=
��
��r=
��
�֡�S��m��n����Բx2+y2=a2������һ�㣬
��m2+n2=a2����r=
��
����ֱ��mx+ny=1�����еĶ�Բ�ķ���Ϊx2+y2=
��
��3��4x2+3y2=1��
��a
| QM |
| QP |
��
|
��P��x0��y0����Բ������һ�㣬
��x02+y02=a2��
��x2+��
| a |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
������C�ķ���Ϊ
| x2 |
| a2 |
| y2 |
| b2 |
��������������ԭ�㣬������x���ϣ����᳤Ϊ2a�����᳤Ϊ2b����Բ��
��2���ɶԳ��ԣ�������Բ����Ϊx2+y2=r2��r��0��
�����⣬��Բ��O��ֱ��l�ľ���d=
| 1 | ||
|
��r=
| 1 | ||
|
�֡�S��m��n����Բx2+y2=a2������һ�㣬
��m2+n2=a2����r=
| 1 |
| a |
����ֱ��mx+ny=1�����еĶ�Բ�ķ���Ϊx2+y2=
| 1 |
| a2 |
��3��4x2+3y2=1��
������������Ҫ����ƽ��������ֱ����Բ����Բ�Ȼ���֪ʶ������������֤�������������������������ʶ�����麯���뷽��˼�롢���ν��˼�롢������ת��˼�롢������һ��˼�룮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 2008��8��18�գ��ڱ������˻��ᄊ������Զ�����У�������ѡ��������ŵ-��������8��34�ijɼ���ùھ���������֪���������ᄊʷ�ϣ�1968��ī������˻ᣬ����ѡ�ֱ���•���ɵ�һ������������8.90�ף�������һ�ɼ���������ʱ�����¼����55���ף�ֱ��23�������������ͻ��������˵ļ�¼����Ϊ����23���������ƴ˼�¼�����ɵ���һ���������ᄊʷ�Ϲ��ԡ������ϰ��������ƣ�ֱ��1991���ڶ������������ϣ�����•����������8.95�ijɼ���������������ġ������ϰ�����������Ծʱ�߶ȵı仯�������ú�����h��t��=-5t2+5t��0��t��1����ʾ��
2008��8��18�գ��ڱ������˻��ᄊ������Զ�����У�������ѡ��������ŵ-��������8��34�ijɼ���ùھ���������֪���������ᄊʷ�ϣ�1968��ī������˻ᣬ����ѡ�ֱ���•���ɵ�һ������������8.90�ף�������һ�ɼ���������ʱ�����¼����55���ף�ֱ��23�������������ͻ��������˵ļ�¼����Ϊ����23���������ƴ˼�¼�����ɵ���һ���������ᄊʷ�Ϲ��ԡ������ϰ��������ƣ�ֱ��1991���ڶ������������ϣ�����•����������8.95�ijɼ���������������ġ������ϰ�����������Ծʱ�߶ȵı仯�������ú�����h��t��=-5t2+5t��0��t��1����ʾ��