已知函数f(x)对任意实数x∈R.f恒成立.且当x∈[-1.1]时.f(x)=2x+a.若点P是该函数图象上一点.则实数a的值为2．题目和参考答案——青夏教育精英家教网—

题目内容

19．已知函数f（x）对任意实数x∈R，f（x+2）=f（x）恒成立，且当x∈[-1，1]时，f（x）=2^x+a，若点P（2017，8）是该函数图象上一点，则实数a的值为2．

分析求出函数的周期，然后利用点的坐标满足函数的解析式，推出结果即可．

解答解：函数f（x）对任意实数x∈R，f（x+2）=f（x）恒成立，可得函数的周期为：2，
f（2017）=f（2×1008+1）=f（1）．且当x∈[-1，1]时，f（x）=2^x+a，
点P（2017，8）是该函数图象上一点，
可得2^1+a=8，解得a=2．
故答案为：2．

点评本题考查抽象函数的应用，函数的解析式以及函数值的求法，考查计算能力．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

$\frac{{{2^{2016}}+1}}{3}$

B．

$\frac{{{2^{2016}}-1}}{3}$

C．

$\frac{{{2^{2017}}+1}}{3}$

D．

$\frac{{{2^{2017}}-1}}{3}$

10．过双曲线x²-$\frac{{y}^{2}}{{b}^{2}}$=1的左顶点A作斜率为1的直线l，若l与双曲线的两条渐近线分别相交于B，C，且2$\overrightarrow{AB}$=$\overrightarrow{BC}$，则此双曲线的离心率是（　　）

A．

$\sqrt{10}$

B．

$\frac{\sqrt{10}}{3}$

7．

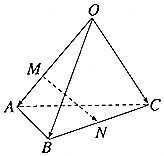如图，四面体OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且OM=2MA，N为BC的中点，$\overrightarrow{MN}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$，则x+y+z=$\frac{1}{3}$．

14．若幂函数y=x^a（a∈R）的图象经过点（4，2），则a的值为$\frac{1}{2}$．

4．

如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．
（1）求|$\overrightarrow{AB}$|；
（2）已知点D是AB上一点，满足$\overrightarrow{AD}$=λ$\overrightarrow{AB}$，点E是边CB上一点，满足$\overrightarrow{BE}$=λ$\overrightarrow{BC}$．
①当λ=$\frac{1}{2}$时，求$\overrightarrow{AE}$•$\overrightarrow{CD}$；
②是否存在非零实数λ，使得$\overrightarrow{AE}$⊥$\overrightarrow{CD}$？若存在，求出的λ值；若不存在，请说明理由．

11．已知抛物线C₁：y²=8x的焦点F到双曲线C₂：$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1，（{a＞0，b＞0}）$的渐近线的距离为$\frac{{4\sqrt{5}}}{5}$，P是抛物线C₁的一动点，P到双曲线C₂的上焦点F₁（0，c）的距离与到直线x+2=0的距离之和的最小值为3，则该双曲线的方程为（　　）

A．

$\frac{y^2}{2}-\frac{x^2}{3}=1$

B．

${y^2}-\frac{x^2}{4}=1$

C．

$\frac{y^2}{4}-{x^2}=1$

D．

$\frac{y^2}{3}-\frac{x^2}{2}=1$

8．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点且垂直于x轴的直线与双曲线交于A，B两点，与双曲线的渐近线交于C，D两点，若|AB|≥$\frac{3}{5}$|CD|，则双曲线离心率的取值范围为[$\frac{5}{4}$，+∞）．

9．

如图，在正方体ABCD-A₁B₁C₁D₁中，点M，N分别是B₁C₁，CC₁的中点，则直线A₁M与DN的位置关系是相交．（填“平行”、“相交”或“异面”）

试题分类