题目内容
7.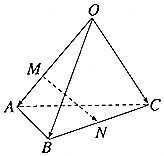 如图,四面体OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且OM=2MA,N为BC的中点,$\overrightarrow{MN}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$,则x+y+z=$\frac{1}{3}$.
如图,四面体OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且OM=2MA,N为BC的中点,$\overrightarrow{MN}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$,则x+y+z=$\frac{1}{3}$.
分析 在四面体OABC中,运用向量的多边形法则,求出$\overrightarrow{MN}$,结合条件由$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示,并由空间向量基本定理,即可得到x,y,z,进而得到所求和.
解答 解:在四面体OABC中,$\overrightarrow{MN}$=$\overrightarrow{MO}$+$\overrightarrow{OC}$+$\overrightarrow{CN}$,
点M在OA上,且OM=2MA,N为BC的中点,
可得$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$=$\frac{2}{3}$$\overrightarrow{a}$,$\overrightarrow{CN}$=$\frac{1}{2}$$\overrightarrow{CB}$=$\frac{1}{2}$($\overrightarrow{OB}$-$\overrightarrow{OC}$)=$\frac{1}{2}$($\overrightarrow{b}$-$\overrightarrow{c}$),
则$\overrightarrow{MN}$=-$\frac{2}{3}$$\overrightarrow{a}$+$\overrightarrow{c}$+$\frac{1}{2}$($\overrightarrow{b}$-$\overrightarrow{c}$)
=-$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$,
又$\overrightarrow{MN}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$,
可得x=-$\frac{2}{3}$,y=z=$\frac{1}{2}$,
则x+y+z=-$\frac{2}{3}$+$\frac{1}{2}$+$\frac{1}{2}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查空间向量和应用,考查多边形法则,以及空间向量基本定理的运用,考查运算能力,属于基础题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
| A. | $\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
| A. | x-2y+1=0 | B. | x+2y+1=0 | C. | x-2y-1=0 | D. | x+2y-1=0 |
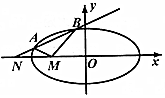 已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).
已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).