题目内容
含2n-1项的等差数列,其奇数项的和与偶数项的和之比为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列的性质和求和公式可得S奇=nan,其偶数项的和S偶=(n-1)an,作比值可得.
解答:
解:∵含2n-1项的等差数列,其奇数项的和S奇=
=
=nan,
其偶数项的和S偶=
=
=(n-1)an,
∴其奇数项的和与偶数项的和之比为
=
故选:B
| n(a1+a2n-1) |
| 2 |
| n•2an |
| 2 |
其偶数项的和S偶=
| (n-1)(a2+a2n-2) |
| 2 |
| (n-1)•2an |
| 2 |
∴其奇数项的和与偶数项的和之比为
| nan |
| (n-1)an |
| n |
| n-1 |
故选:B
点评:本题考查等差数列的求和公式和性质,属基础题.

练习册系列答案
相关题目
在△A BC中,“
•
>0”是“△ABC为锐角三角形”的( )
| AB |
| AC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
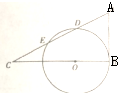 如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=
如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=