题目内容
已知函数f（x）=2x2+3x-5．
（1）求当x1=4，且△x=1时，函数增量△y和平均变化率
；
（2）求当x1=4，且△x=0.1时，函数增量△x和平均变化率
．
（1）求当x1=4，且△x=1时，函数增量△y和平均变化率
| △y |
| △x |
（2）求当x1=4，且△x=0.1时，函数增量△x和平均变化率
| △y |
| △x |
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：先化简函数增量△y和平均变化率
，再代入数值计算即可．
| △y |
| △x |
解答：
解：△y=f（x1+△x）-f（x1）=2（x1+△x）2+3（x1+△x）-5-2x12-3x1+5=2△x2+4x1△x+3△x，
=2△x+4x1+3，
（1）当x1=4，且△x=1时，△y=2+16+3=21，
=2+16+3=21，
（2）当x1=4，且△x=0.1时，△y=0.02+1.6+0.3=1.92，
=0.2+16+3=19.2，
| △y |
| △x |
（1）当x1=4，且△x=1时，△y=2+16+3=21，
| △y |
| △x |
（2）当x1=4，且△x=0.1时，△y=0.02+1.6+0.3=1.92，
| △y |
| △x |
点评：本题考查了函数的平均数变化率的问题，属于基础题．
练习册系列答案
相关题目
若-
＜α＜-
，从单位圆中的三角函数线观察sinα，cosα，tanα的大小是（ ）
| 3π |
| 4 |
| π |
| 2 |
| A、sinα＜tanα＜cosα |
| B、cosα＜sinα＜tanα |
| C、sinα＜coasα＜tanα |
| D、tanα＜sinα＜cosα |
含2n-1项的等差数列，其奇数项的和与偶数项的和之比为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线a∥平面α，直线a⊥平面β，则（ ）
| A、α⊥β | B、α∥β |
| C、α与β不垂直 | D、以上都有可能 |
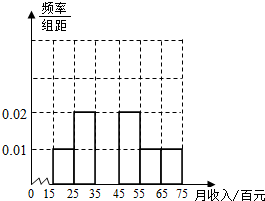为了解某市民众对某项公共政策的态度，在该市随机抽取了50名市民进行调查，做出了他们的月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到他们月收入情况以及对该项政策赞成的人数统计表：