题目内容
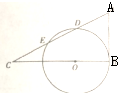如图，圆O的圆心在Rt△ABC的直角边BC上，该圆与直角边AB相切，与斜边AC交于点D、E，AD=DE=EC，AB=| 14 |
考点：与圆有关的比例线段
专题：推理和证明
分析：由切割线定理得AB2=AD•（AD+DE），从而得到AD=DE=EC=
，由此利用勾股定理能求出BC．
| 7 |
解答：
解：∵AB是切线，ADE是割线，
∴AB2=AD•（AD+DE），
∵AB=
，AD=DE=EC，
∴(
)2=AD•2AD，解得AD=DE=EC=
，
∴AC=3
，
∵Rt△ABC的直角为∠ABC，
∴BC=
=
=7．
故答案为：7．
∴AB2=AD•（AD+DE），
∵AB=
| 14 |
∴(
| 14 |
| 7 |
∴AC=3
| 7 |
∵Rt△ABC的直角为∠ABC，
∴BC=
| AC2-AB2 |
| 63-14 |
故答案为：7．
点评：本题考查直角边的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
相关题目
含2n-1项的等差数列，其奇数项的和与偶数项的和之比为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，若A＜B＜C，b=10，且a+c=2b，C=2A，则a与c的值分别为（ ）
| A、8，10 | B、10，10 |
| C、8，12 | D、12，8 |
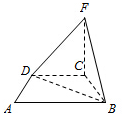一几何体如图所示，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°．FC⊥平面ABCD，CB=CD=CEF=1．