题目内容
化简：cos2（α+45°）-sin2（α+45°）= ．
考点：三角函数的化简求值
专题：计算题,三角函数的求值
分析：运用二倍角的余弦公式和诱导公式，化简即可得到．
解答：
解：cos2（α+45°）-sin2（α+45°）
=cos2（α+45°）=cos（2α+90°）=-sin2α．
故答案为：-sin2α．
=cos2（α+45°）=cos（2α+90°）=-sin2α．
故答案为：-sin2α．
点评：本题考查三角函数的化简，主要考查二倍角的余弦公式和诱导公式的运用，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
已知m＞0，n＞0，向量
=(1，1)，向量
=(m，n-3)，且
⊥(
+
)，则
+
的最小值为（ ）
| a |
| b |
| a |
| a |
| b |
| 1 |
| m |
| 4 |
| n |
| A、9 | B、16 | C、18 | D、8 |
含2n-1项的等差数列，其奇数项的和与偶数项的和之比为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线a∥平面α，直线a⊥平面β，则（ ）
| A、α⊥β | B、α∥β |
| C、α与β不垂直 | D、以上都有可能 |
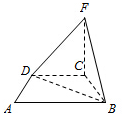一几何体如图所示，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°．FC⊥平面ABCD，CB=CD=CEF=1．在函数f（x）=
，则f（log310）=（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
={3，4}，
•
=5，|
-
|=2
，则|
|=（ ）
| b |
| a |
| b |
| a |
| b |
| 5 |
| a |
| A、5 | ||
| B、25 | ||
C、2
| ||
D、
|