题目内容
已知向量
=(1,1),
=(-1,k).(2
+
)•
=5,则实数k= .
| a |
| b |
| a |
| b |
| a |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的数量积运算即可得出.
解答:
解:∵向量
=(1,1),
=(-1,k).
∴2
+
=(2,2)+(-1,k)=(1,2+k).
∴(2
+
)•
=1+2+k=5,
解得k=2.
故答案为:2.
| a |
| b |
∴2
| a |
| b |
∴(2
| a |
| b |
| a |
解得k=2.
故答案为:2.
点评:本题考查了向量的坐标运算及其数量积运算,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知m>0,n>0,向量
=(1,1),向量
=(m,n-3),且
⊥(
+
),则
+
的最小值为( )
| a |
| b |
| a |
| a |
| b |
| 1 |
| m |
| 4 |
| n |
| A、9 | B、16 | C、18 | D、8 |
若-
<α<-
,从单位圆中的三角函数线观察sinα,cosα,tanα的大小是( )
| 3π |
| 4 |
| π |
| 2 |
| A、sinα<tanα<cosα |
| B、cosα<sinα<tanα |
| C、sinα<coasα<tanα |
| D、tanα<sinα<cosα |
含2n-1项的等差数列,其奇数项的和与偶数项的和之比为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在函数f(x)=
,则f(log310)=( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
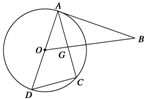 如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.求证:BA•DC=GC•AD.
如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.求证:BA•DC=GC•AD.