已知圆锥的底面半径和高均为1.则该圆锥的侧面积为$\sqrt{2}π$．题目和参考答案——青夏教育精英家教网—

题目内容

2．已知圆锥的底面半径和高均为1，则该圆锥的侧面积为$\sqrt{2}π$．

分析首先根据底面半径和高利用勾股定理求得母线长，然后直接利用圆锥的侧面积公式代入求出即可．

解答解：∵圆锥的底面半径为1，高为1，
∴母线长l为：$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，
∴圆锥的侧面积为：πrl=π×1×$\sqrt{2}$=$\sqrt{2}$π，
故答案为：$\sqrt{2}$π．

点评题考查了圆锥的侧面积的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

13．湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下了一个半径为4cm，深2cm的空穴，则该球表面积为（　　） cm²．

10．设a=log₂$\frac{1}{3}$，b=（$\frac{1}{2}$）³，c=3${\;}^{\frac{1}{2}}$，则（　　）

17．已知全集U=R，函数$f（x）=\sqrt{x-3}+lg（{10-x}）$的定义域为集合A，集合B={x|5≤x＜7}
（1）求集合A；
（2）求（∁_UB）∩A．

7．若变量x、y满足约束条件$\left\{\begin{array}{l}{x+y≤12}\\{2x-y≥0}\\{x-2y≤0}\end{array}\right.$，则z=y-x的最小值为-4．

14．有三张卡片，分别写有1和2，1和3，2和3，甲乙丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上没有的数字是（　　）

11．已知椭圆$C：\frac{x^2}{a^2}+{y^2}=1（a＞1）$，离心率$e=\frac{{\sqrt{6}}}{3}$．直线l：x=my+1与x轴交于点A，与椭圆C相交于E，F两点．自点E，F分别向直线x=3作垂线，垂足分别为E₁，F₁．
（Ⅰ）求椭圆C的方程及焦点坐标；
（Ⅱ）记△AEE₁，△AE₁F₁，△AFF₁的面积分别为S₁，S₂，S₃，试证明$\frac{{{S_1}{S_3}}}{{{S_2}^2}}$为定值．

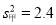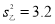甲、乙两人在相同的条件下各射靶10次，他们的环数的方差分别为：，，则射击稳定程度是

A．甲高 B．乙高 C．两人一样高 D．不能确定

试题分类