题目内容
7.若变量x、y满足约束条件$\left\{\begin{array}{l}{x+y≤12}\\{2x-y≥0}\\{x-2y≤0}\end{array}\right.$,则z=y-x的最小值为-4.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≤12}\\{2x-y≥0}\\{x-2y≤0}\end{array}\right.$作出可行域如图,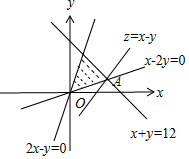
联立$\left\{\begin{array}{l}{x+y=12}\\{x-2y=0}\end{array}\right.$,解得A(8,4),
化目标函数z=y-x,得y=x+z,
由图可知,当直线y=x+z过点A(8,4)时,直线在y轴上的截距最小,z有最小值为-4.
故答案为:-4.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
17.2016世界特色魅力城市200强新鲜出炉,包括黄山市在内的28个中国城市入选.美丽的黄山风景和人文景观迎来众多宾客.现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:
(1)若在100这人中,按性别分层抽取一个容量为20的样本,女性应抽11人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过0.05前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节游客中随机抽取3人赠送精美纪念品,记这3人中赞成“自助游”人数为X,求X的分布列和数学期望.
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$
| 赞成“自助游” | 不赞成“自助游” | 合计 | |
| 男性 | 30 | ||
| 女性 | 10 | ||
| 合计 | 100 |
(2)若以抽取样本的频率为概率,从旅游节游客中随机抽取3人赠送精美纪念品,记这3人中赞成“自助游”人数为X,求X的分布列和数学期望.
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
15.若区间[x1,x2]的 长 度 定 义 为|x2-x1|,函数f(x)=$\frac{({m}^{2}+m)x-1}{{m}^{2}x}$(m∈R,m≠0)的定义域和值域都是[a,b],则区间[a,b]的最大长度为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 3 |
16.已知数列1,a,5是等差数列,则实数a的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{5}$ |
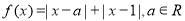 .
.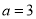 时,解不等式
时,解不等式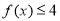 ;
;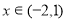 时,
时,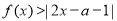 ,求
,求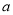 的取值范围.
的取值范围.