题目内容
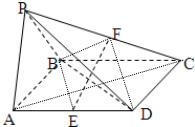 已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=
已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=| 1 |
| 2 |
(1)求证:EF⊥平面PBD;
(2)求三棱锥C-BEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取PB的中点为M连结AM,MF,由已知得AB⊥BD,AM⊥BD,从而AM⊥面PBD,由EF∥AM,能证明EF⊥面PBD.
(2)先求出S△BEC=
×BE×EC=2
,作PH⊥AB,连结CH,作FO⊥CH,FO
AH=
,由此能求出三棱锥C-BEF的体积.
(2)先求出S△BEC=
| 1 |
| 2 |
| 3 |
| ∥ |
. |
| 1 |
| 2 |
| ||
| 2 |
解答:
(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,
所以FM
BC,又ABCD是平行四边形,
E为AD的中点,所以AMFE是平行四边形,
所以EF∥面PAB,
因为△PAB为正三角形,且AB=
AD=2,
M是PB的中点,所以AM⊥PB,∠BAD=60°,
所以AB⊥BD,
因为面PAB⊥面ABCD,所以BD⊥平面PAB,
所以AM⊥BD,
又PB∩BD=B,所以AM⊥面PBD.EF∥AM,
所以EF⊥面PBD.
(2)解:由∠EBC=120°-60°=60°,DE=DC,且∠CDE=120°,
得∠ECD=30°,从而∠BEC=90°,
∴S△BEC=
×BE×EC=2
,
作PH⊥AB,交AB于H,则H是AB中点,连结CH,作FO⊥CH,交CH于O,
则FO
AH=
,
∵面PAB⊥面ABCD,∴AH⊥平面ABCD,∴FO⊥平面ABCD,
∴三棱锥C-BEF的体积V=
×FO×S△BEF=
×
×2
=1.
所以FM
| ∥ |
. |
| 1 |
| 2 |

E为AD的中点,所以AMFE是平行四边形,
所以EF∥面PAB,
因为△PAB为正三角形,且AB=
| 1 |
| 2 |
M是PB的中点,所以AM⊥PB,∠BAD=60°,
所以AB⊥BD,
因为面PAB⊥面ABCD,所以BD⊥平面PAB,
所以AM⊥BD,
又PB∩BD=B,所以AM⊥面PBD.EF∥AM,
所以EF⊥面PBD.
(2)解:由∠EBC=120°-60°=60°,DE=DC,且∠CDE=120°,
得∠ECD=30°,从而∠BEC=90°,
∴S△BEC=
| 1 |
| 2 |
| 3 |
作PH⊥AB,交AB于H,则H是AB中点,连结CH,作FO⊥CH,交CH于O,
则FO
| ∥ |
. |
| 1 |
| 2 |
| ||
| 2 |
∵面PAB⊥面ABCD,∴AH⊥平面ABCD,∴FO⊥平面ABCD,
∴三棱锥C-BEF的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
点评:本题考查异面直线垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
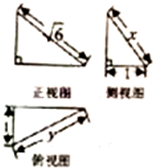
某几何体的三视图如图所示,则t=x-y的取值范围是( )

| A、[-4,4] | ||||
| B、(-1,1) | ||||
| C、[-1,1] | ||||
D、(1-
|
已知an=-2n2+9n+3,则数列{an}中的最大项为( )
| A、a1=10 |
| B、a2=13 |
| C、a3=12 |
| D、以上均不正确 |
已知点M(a,b)在圆O:x2+y2=1内,则直线l:ax+by=1与圆O的位置关系是( )
| A、相切 | B、相交 | C、相离 | D、不确定 |
将函数y=2sin2x图象上的所有点向右平移
个单位,然后把图象上所有点的横坐标缩短为原来的
倍,(纵坐标不变)得到y=f(x)的图象,则f(x)等于( )
| π |
| 6 |
| 1 |
| 2 |
A、2sin(x-
| ||
B、2sin(x-
| ||
C、2sin(4x-
| ||
D、2sin(4x-
|