题目内容
当f(x)=
+
,当x为何值,f(x)为最大值.
| 5+x |
| 5-x |
考点:函数的最值及其几何意义
专题:计算题,不等式的解法及应用
分析:利用基本不等式的变形式得(
)2≤
=5;从而确定最值点.
| ||||
| 2 |
| ||||
| 2 |
解答:
解:∵(
)2≤
=5;
(当且仅当
=
,即x=0时,等号成立)
∴
+
≤2
.
故当x=0时,f(x)取得最大值.
| ||||
| 2 |
| ||||
| 2 |
(当且仅当
| 5+x |
| 5-x |
∴
| 5+x |
| 5-x |
| 5 |
故当x=0时,f(x)取得最大值.
点评:本题考查了基本不等式在求最值时的应用,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
已知cos(60°+α)=
,且α为第三象限角,则cos(30°-α)+sin(30°-α)的值为( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题“若函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,则loga2<0”的逆否命题是( )
| A、若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 |
| B、若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数 |
| C、若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 |
| D、若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数 |
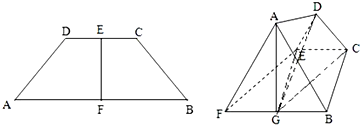
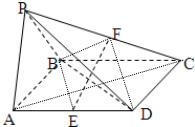 已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=
已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=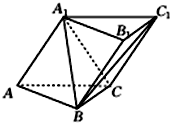 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.