题目内容
将函数y=2sin2x图象上的所有点向右平移
个单位,然后把图象上所有点的横坐标缩短为原来的
倍,(纵坐标不变)得到y=f(x)的图象,则f(x)等于( )
| π |
| 6 |
| 1 |
| 2 |
A、2sin(x-
| ||
B、2sin(x-
| ||
C、2sin(4x-
| ||
D、2sin(4x-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:直接由函数图象的平移得答案.
解答:
解:将函数y=2sin2x图象上所有点向右平移
个单位,所得图象的解析式为y=2sin(2x-
),
然后把所得图象上所有点的横坐标缩短到原来的
倍(纵坐标不变),得到y=f(x)的图象的解析式为f(x)=2sin(4x-
).
故选:D.
| π |
| 6 |
| π |
| 3 |
然后把所得图象上所有点的横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 3 |
故选:D.
点评:本题考查了y=Asin(ωx+φ)型函数图象的平移,注意变化顺序是关键,是中档题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知命题p:“x>3”是“x2>9”的充要条件,命题q:“?x0∈R,x0-2>0”的否定是“?x0∈R,x0-2<0”( )
| A、“p∨q”为真 |
| B、“p∧q”为真 |
| C、p真q假 |
| D、p,q均为假 |
已知cos(60°+α)=
,且α为第三象限角,则cos(30°-α)+sin(30°-α)的值为( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中,真命题是( )
| A、?x∈R,sinx+cosx>2 | ||
| B、m2+n2=0(m,n∈R),则m=0且n=0 | ||
| C、“x=4”是“x2-3x-4=0”的充要条件 | ||
D、“0<ab<1”是“b<
|
 2014年巴西世界杯刚结束,某足球协会为了调查球迷对本届世界杯的了解情况,组织了“世界杯你问我答一百问”活动,该协会从参加活动的球迷(人数不少于1000人)中随机抽取12名球迷.进行世界杯知识问卷测试,测试成绩(百分制)以茎叶图形式表示如右图所示,根据主办方标准.测试成绩低于80分的为“伪球迷”,不低于80分的为“真球迷”.
2014年巴西世界杯刚结束,某足球协会为了调查球迷对本届世界杯的了解情况,组织了“世界杯你问我答一百问”活动,该协会从参加活动的球迷(人数不少于1000人)中随机抽取12名球迷.进行世界杯知识问卷测试,测试成绩(百分制)以茎叶图形式表示如右图所示,根据主办方标准.测试成绩低于80分的为“伪球迷”,不低于80分的为“真球迷”.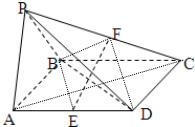 已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=
已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=