题目内容
已知点M(a,b)在圆O:x2+y2=1内,则直线l:ax+by=1与圆O的位置关系是( )
| A、相切 | B、相交 | C、相离 | D、不确定 |
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:先求圆心到直线ax+by=1的距离,通过关系判断点P(a,b)与圆的位置关系.
解答:
解:∵点P(a,b)是圆x2+y2=1内不同于原点的一点,
∴
<1,
∵圆心到直线ax+by=1的距离,d=
>1.
故直线和圆相离.
故选:C.
∴
| a2+b2 |
∵圆心到直线ax+by=1的距离,d=
| 1 | ||
|
故直线和圆相离.
故选:C.
点评:本题考查直线和圆的位置关系,点与圆的位置关系,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
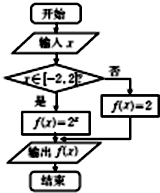 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、[-2,-1] |
| B、(-∞,-1] |
| C、[-1,2] |
| D、[2,+∞) |
已知命题p:“x>3”是“x2>9”的充要条件,命题q:“?x0∈R,x0-2>0”的否定是“?x0∈R,x0-2<0”( )
| A、“p∨q”为真 |
| B、“p∧q”为真 |
| C、p真q假 |
| D、p,q均为假 |
已知直线kx-y=k-1与直线ky-x=2k,若0<k<
,则它们的交点在( )
| 1 |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
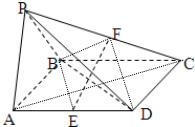 已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB=
已知四棱锥P-ABCD是底面为平行四边形,面PAB⊥面ABCD,△PAB为正三角形,且AB= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=