题目内容
已知椭圆的焦点为(-4,0),(4,0),椭圆上一点 P到两个焦点的距离之和为10,则椭圆方程为 .
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由条件可得c=4,由定义可得a=5,再由a,b,c的关系,可得b=3,进而得到椭圆方程.
解答:
解:由于椭圆的焦点为(-4,0),(4,0),
则c=4,
由椭圆上一点P到两个焦点的距离之和为10,
则2a=10,解得,a=5,
则b2=a2-c2=9,
则椭圆方程为
+
=1.
故答案为:
+
=1.
则c=4,
由椭圆上一点P到两个焦点的距离之和为10,
则2a=10,解得,a=5,
则b2=a2-c2=9,
则椭圆方程为
| x2 |
| 25 |
| y2 |
| 9 |
故答案为:
| x2 |
| 25 |
| y2 |
| 9 |
点评:本题考查椭圆的定义和方程,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知 p:“一个有理数与一个无理数的和是无理数”,q:“一个有理数与一个无理数的积是无理数”,则命题 p、q、p∧q中的真命题是( )
| A、p | B、q |
| C、p∧q | D、p、q、p∧q |
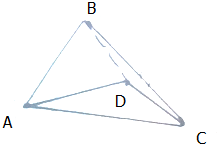 如图,在四面体ABCD中,△ABD是正三角形,AB⊥BC,AD⊥DC,AC=2AB,则直线DC与平面ABD所成角的正弦值等于
如图,在四面体ABCD中,△ABD是正三角形,AB⊥BC,AD⊥DC,AC=2AB,则直线DC与平面ABD所成角的正弦值等于