题目内容

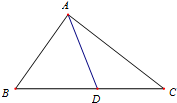如图，在△ABC中，已知B=45°，D是BC上一点，AD=10，AC=14，DC=6，则AB=
 
．
考点：解三角形的实际应用
专题：解三角形
分析：根据余弦定理弦求出C的大小，利用正弦定理即可求出AB的长度．
解答： 解：∵AD=10，AC=14，DC=6，
∴由余弦定理得cosC=
AC2+CD2-AD2
2AC•CD
=
142+62-102
2×14×6
=
11
14
，
∴sinC=
1-(
11
14
)2
=
5
3
14
，
由正弦定理得
AB
sinC
=
AC
sinB
，
即AB=
AC•sinC
sinB
=
14×
5
3
14
2
2
=5
6
，
故答案为：5
6
点评：本题主要考查解三角形的应用，利用余弦定理和正弦定理是解决本题的关键，要求熟练掌握相应的公式．
练习册系列答案
相关题目
圆C1：（x+1）2+y2=1与圆C2：（x-3）2+（y-4）2=1的位置关系是
 
．
已知f（x）=
(sinx+cosx)2
2+2sin2x-cos22x
，若f（
3π
8
+
α
2
）=
13
18
，f（
π
8
-
β
2
）=5，且0＜α＜
π
4
，
π
4
＜β＜
3π
4
，则sin（α+β）的值为
 
．
将一个等差数列依次写成下表：
第一行：2
第二行：5，8，11
第三行：14，17，20，23，26
…
第m行：a（m，1），a（m，2），a（m，3），…，a（m，2m-1）
其中a（i，j）表示第i行中的第j个数，那么第m行的数的和是
 
．
已在△ABC中，b2-bc-2c2=0，a=
6
，cosA=
7
8
，则△ABC的面积S为
 
．
设点P为△ABC的边BC上的一点，且满足
AP
=
1
4
AB
-
3
4
CA
，则△ABP与△APC的面积之比为
 
．
已知集合A={a1，a2，a3}，B={b1，b2，b3}，f：A→B为集合A到B的一个函数，那么该函数的值域C的不同情况有
 
种．
已知在△ABC中满足：tanA•tanB=1+
3
（tanA+tanB），则角C等于（　　）
A、
π
6
B、
π
3
C、
2π
3
D、
5
6
π
如果对定义在R上的函数f（x），对任意x1≠x2，都有x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1）则称函数f（x）为“H函数”．给出下列函数：
①y=-x3+x+1；
②y=3x-2（sinx-cosx）；
③y=ex+1；
④f（x）=
ln|x|，x≠0
0，x=0
．
其中函数式“H函数”的个数是（　　）
A、4B、3C、2D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网