题目内容
将一个等差数列依次写成下表:
第一行:2
第二行:5,8,11
第三行:14,17,20,23,26
…
第m行:a(m,1),a(m,2),a(m,3),…,a(m,2m-1)
其中a(i,j)表示第i行中的第j个数,那么第m行的数的和是 .
第一行:2
第二行:5,8,11
第三行:14,17,20,23,26
…
第m行:a(m,1),a(m,2),a(m,3),…,a(m,2m-1)
其中a(i,j)表示第i行中的第j个数,那么第m行的数的和是
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:先确定a(m,1),再利用等差数列的求和公式,即可得出结论.
解答:
解:由题意,每行的首数分别为2,5,14,…
则a(m,1)=2+3+9+15+…+[3+6(m-2)]=2+
=3(m-1)2+2,
∴第m行的数的和是(2m-1)[3(m-1)2+2]+
×3=(2m-1)(3m2-3m+2).
故答案为:(2m-1)(3m2-3m+2).
则a(m,1)=2+3+9+15+…+[3+6(m-2)]=2+
| (m-1)[3+3+6(m-2)] |
| 2 |
∴第m行的数的和是(2m-1)[3(m-1)2+2]+
| (2m-1)(2m-2) |
| 2 |
故答案为:(2m-1)(3m2-3m+2).
点评:本题考查等差数列的通项与求和,考查学生的计算能力,确定a(m,1)是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将4名学生分配到甲、乙、丙3个实验室准备实验,每个实验室至少分配1名学生的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
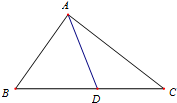 如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=
如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=