题目内容
已知f(x)=
,若f(
+
)=
,f(
-
)=5,且0<α<
,
<β<
,则sin(α+β)的值为 .
| (sinx+cosx)2 |
| 2+2sin2x-cos22x |
| 3π |
| 8 |
| α |
| 2 |
| 13 |
| 18 |
| π |
| 8 |
| β |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由题,解析式可化简为f(x)=
=
=
=
,再化简f(
+
)=
,f(
-
)=5,即可观察出求sin(α+β)的值的方法.
| (sinx+cosx)2 |
| 2+2sin2x-cos22x |
| 1+sin2x |
| 2+2sin2x-cos22x |
| 1+sin2x |
| 1+2sin2x+sin22x |
| 1 |
| 1+sin2x |
| 3π |
| 8 |
| α |
| 2 |
| 13 |
| 18 |
| π |
| 8 |
| β |
| 2 |
解答:
角:∵f(x)=
=
=
=
,
∴f(
+
)=
=
,解得sin(
+α)=
,
f(
-
)=
=5,解得sin(
-β)=-
,
又0<α<
,
<β<
,
∴
+α∈(
,π),
-β∈(-
,0),
∴cos(
+α)=-
,cos(
-β)=
,
∴sin(α+β)=sin[
+α-(
-β)-
]
=-cos[
+α-(
-β)]
=-[cos(
+α)cos(
-β)+sin(
+α)sin(
-β)]
=-[-
×
+
×(-
]
=
.
故答案为:
| (sinx+cosx)2 |
| 2+2sin2x-cos22x |
| 1+sin2x |
| 2+2sin2x-cos22x |
| 1+sin2x |
| 1+2sin2x+sin22x |
| 1 |
| 1+sin2x |
∴f(
| 3π |
| 8 |
| α |
| 2 |
| 1 | ||
1+sin(
|
| 13 |
| 18 |
| 3π |
| 4 |
| 5 |
| 13 |
f(
| π |
| 8 |
| β |
| 2 |
| 1 | ||
1+sin(
|
| π |
| 4 |
| 4 |
| 5 |
又0<α<
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴
| 3π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴cos(
| 3π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
| 3 |
| 5 |
∴sin(α+β)=sin[
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
=-cos[
| 3π |
| 4 |
| π |
| 4 |
=-[cos(
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
=-[-
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
=
| 56 |
| 65 |
故答案为:
| 56 |
| 65 |
点评:本题考查三角恒等变换公式的应用,利用三角恒等变换公式求值熟练掌握公式很关键,本题考查了用已知表示未知的变换思想,这是三角函数求值中常用的技巧

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
定义两种运算a⊕b=ab,a?b=a2+b2,则f(x)=
为( )
| 2⊕x |
| x?2-2 |
| A、奇函数 |
| B、偶函数 |
| C、既不是奇函数又不是偶函数 |
| D、既是奇函数又是偶函数 |
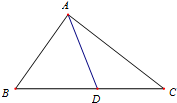 如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=
如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=