题目内容
已知集合A={a1,a2,a3},B={b1,b2,b3},f:A→B为集合A到B的一个函数,那么该函数的值域C的不同情况有 种.
考点:映射
专题:计算题,函数的性质及应用
分析:利用映射的定义及性质,推断出集合B中所有元素的像的集合为函数的值域C,进而通过枚举的方法得出答案.
解答:
解:∵满映射f:A→B是一个函数,其中原像集A称做函数的定义域,像集B称做函数的值域,
∴集合B中所有元素的像的集合为函数的值域C
∴值域C有可能是{b1},{b2},{b3},{b1,b2},{b2,b3},{b1,b3},{b1,b2,b3},共7中可能.
故答案为:7
∴集合B中所有元素的像的集合为函数的值域C
∴值域C有可能是{b1},{b2},{b3},{b1,b2},{b2,b3},{b1,b3},{b1,b2,b3},共7中可能.
故答案为:7
点评:本题主要考查学生对映射定义及性质的理解和运用.注意映射与函数知识的关联.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
已知a>0且a≠1,函数f(x)=
满足对任意实数x1≠x2,都有
>0成立,则a的取值范围是( )
|
| f(x2)-f(x1) |
| x2-x1 |
| A、(0,1) | ||
| B、(1,+∞) | ||
C、(1,
| ||
D、[
|
定义两种运算a⊕b=ab,a?b=a2+b2,则f(x)=
为( )
| 2⊕x |
| x?2-2 |
| A、奇函数 |
| B、偶函数 |
| C、既不是奇函数又不是偶函数 |
| D、既是奇函数又是偶函数 |
下列函数满足|x|≥|f(x)|的是( )
| A、f(x)=ex-1 |
| B、f(x)=ln(x+1) |
| C、f(x)=tanx |
| D、f(x)=sinx |
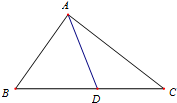 如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=
如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=