题目内容
已知直线l的极坐标方程为ρ=
,点P的直角坐标为(
cosθ,sinθ),求点P到直线l距离的最大值及最小值.
4
| ||
cos(θ+
|
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,求出点P(
cosθ,sinθ)到直线l距离d=
,再利用余弦函数的值域,求得点P到直线l距离的最大值及最小值.
| 3 |
|2cos(θ+
| ||
|
解答:
解:直线l的极坐标方程为ρ=
,化为直角坐标方程为
x-
y=4
,
即 x-y-8=0.
∵点P(
cosθ,sinθ)到直线l距离d=
=
,
故d的最大值为
=5
,d的最小值为
=3
.
4
| ||
cos(θ+
|
| ||
| 2 |
| ||
| 2 |
| 2 |
即 x-y-8=0.
∵点P(
| 3 |
|
| ||
|
|2cos(θ+
| ||
|
故d的最大值为
| |-2-8| | ||
|
| 2 |
| |2-8| | ||
|
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,余弦函数的值域,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
由a1=1,an+1=
给出的数列{an}的第34项是( )
| an |
| 3an+1 |
A、
| ||
| B、100 | ||
C、
| ||
D、
|
某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算的K2≈3.918,经查对下面的临界值表,我们( )
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A、至少有95%的把握认为“这种血清能起到预防感冒的作用” |
| B、至少有99%的把握认为“这种血清能起到预防感冒的作用” |
| C、至少有97.5%的把握认为“这种血清能起到预防感冒的作用” |
| D、没有充分理由说明“这种血清能起到预防感冒的作用” |
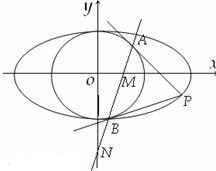 已知椭圆
已知椭圆