题目内容
一半径为r的圆内切于半径为3r、圆心角为α（0＜α＜
）的扇形，则该圆的面积与该扇形的面积之比为（ ）
| π |
| 2 |
| A、3：4 | B、2：3 |
| C、1：2 | D、1：3 |
考点：扇形面积公式
专题：计算题,三角函数的求值
分析：首先求出扇形圆心角，进而利用扇形面积公式求出扇形面积，即可得出圆的面积与该扇形的面积之比．
解答：
解：设⊙O与扇形相切于点A，B，
则AO=r，CO=2r
∴CO=2AO=2，
∴∠ACO=30°，
∴扇形的圆心角为60°=
，
∴扇形的面积为
•
•3r•3r=
πr2，
∵圆的面积为πr2，
∴圆的面积与该扇形的面积之比为2：3．
故选：B．
解：设⊙O与扇形相切于点A，B，则AO=r，CO=2r
∴CO=2AO=2，
∴∠ACO=30°，
∴扇形的圆心角为60°=
| π |
| 3 |
∴扇形的面积为
| 1 |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
∵圆的面积为πr2，
∴圆的面积与该扇形的面积之比为2：3．
故选：B．
点评：此题主要考查了相切两圆的性质以及扇形弧长、面积公式等知识，根据已知得出扇形圆心角是解题关键．
练习册系列答案
相关题目
各项都为正数的等比数列{an}中，a1=2，a3=8，则公比q的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
已知圆C：（x-2）2+（y-b）2=r2（b＞0）经过点（1，0），且圆C被x、y轴截得的弦长之比为1：
，则b和r的值分别是（ ）
| 3 |
A、b=
| ||||
B、b=
| ||||
C、b=
| ||||
D、b=4，r=
|
由a1=1，an+1=
给出的数列{an}的第34项是（ ）
| an |
| 3an+1 |
A、
| ||
| B、100 | ||
C、
| ||
D、
|
设全集U=R，集合M={y|y=2x，x∈R}，N={x|log3（x+2）＜1}，则M∩N等于（ ）
| A、{x|-2＜x≤0} |
| B、{x|0＜x＜1} |
| C、{x|x≥1} |
| D、∅ |
在复平面内，复数
（i是虚数单位）所对应的点位于（ ）
| 2 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
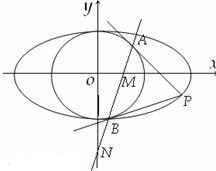已知椭圆