题目内容
调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表:
利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?(注:x2=
)
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:根据所给的表格中的数据,代入求观测值的公式求出观测值,同临界值进行比较,得到有99.9%的把握认为“患桑毛虫皮炎病与采桑”有关系.
解答:
解:因为n11=18,n12=12,n21=5,n22=78,
所以n1+=30,n2+=83,n+1=23,n+2=90,n=113.
所以χ2=
≈39.6>6.635.
所以有99%的把握认为“患桑毛虫皮炎病与采桑”有关系.认为两者有关系会犯错误的概率是1%.
所以n1+=30,n2+=83,n+1=23,n+2=90,n=113.
所以χ2=
| 113×(18×78-5×12)2 |
| 30×82×23×90 |
所以有99%的把握认为“患桑毛虫皮炎病与采桑”有关系.认为两者有关系会犯错误的概率是1%.
点评:本题考查独立性检验知识及应用,考查学生的计算能力,考查学生分析解决问题的能力.

练习册系列答案
相关题目
已知圆C:(x-2)2+(y-b)2=r2(b>0)经过点(1,0),且圆C被x、y轴截得的弦长之比为1:
,则b和r的值分别是( )
| 3 |
A、b=
| ||||
B、b=
| ||||
C、b=
| ||||
D、b=4,r=
|
函数y=sin(x+
)的一个单调增区间是( )
| π |
| 4 |
| A、[-π,0] | ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
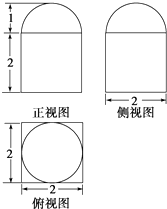 某个几何体的三视图如图所示(单位:m),
某个几何体的三视图如图所示(单位:m),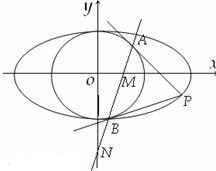 已知椭圆
已知椭圆