题目内容
已知:数列bn=
,数列{bn}前n项和Tn.求证:Tn<
.
| n+1 |
| (n+2)2•4n2 |
| 5 |
| 64 |
考点:数列与不等式的综合
专题:证明题,等差数列与等比数列
分析:bn=
=
(
-
),求和,即可证明结论.
| n+1 |
| (n+2)2•4n2 |
| 1 |
| 16 |
| 1 |
| n2 |
| 1 |
| (n+2)2 |
解答:
证明:bn=
=
[
-
],
∴Tn=
[1-
+
-
+
-
+
-
+…+
-
]
=
[1+
-
-
]<
.
| n+1 |
| (n+2)2•4n2 |
| 1 |
| 16 |
| 1 |
| n2 |
| 1 |
| (n+2)2 |
∴Tn=
| 1 |
| 16 |
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 9 |
| 1 |
| 25 |
| 1 |
| 16 |
| 1 |
| 36 |
| 1 |
| n2 |
| 1 |
| (n+2)2 |
=
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| (n+1)2 |
| 1 |
| (n+2)2 |
| 5 |
| 64 |
点评:本题考查数列与不等式的综合,考查学生分析解决问题的能力,正确裂项是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
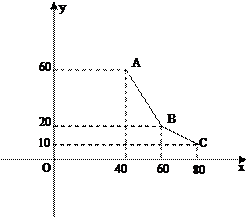 小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元. 如图,在正方形ABCD中,E为AB的中点,P为线段BD上的任意一点,设向量
如图,在正方形ABCD中,E为AB的中点,P为线段BD上的任意一点,设向量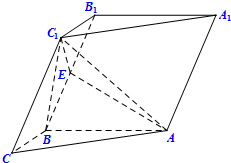 如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=