Question

某种产品的广告费用支出x（万元）与销售额y（万元）之间有如下的对应数据：

x	2	4	5	6	8
y	30	40	60	50	70

（1）在给出的直角坐标系中画出散点图；
（2）求回归直线方程；
（3）据此估计广告费用为10万元时，销售收入y的值．
参考公式：回归直线的方程

?

y

=bx+a，其中b=

n i=1 (xi- . x )(yi- . y )

n i=1 (xi- . x )2

=

n i=1 xiyi-n . x . y

n i=1 x 2 i -n . x 2

，a=

.

y

-b

.

x

参考数据：

5

i=1

x

2 i

=145，

5

i=1

y

2 i

=13500，

5

i=1

xiyi=1380．

Answer 1

考点：线性回归方程

专题：概率与统计

分析：（1）利用已知条件，直接在给出的直角坐标系中画出散点图即可；
（2）求出回归直线方程中的a，b，即可求回归直线方程；
（3）利用广告费用为10万元时，代入回归直线方程即可求出销售收入y的值．

解答： （本小题满分14分）
解：（1）作出散点图如下图所示：
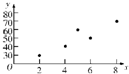…（5分）
（2）

.

x

=

1

5

×(2+4+5+6+8)=5，

.

y

=

1

5

×(30+40+60+50+70)=50…（7分）

b

=

∑xiyi-5 . x . y

∑xi2-5 . x 2

=

1380-5×5×50

145-5×52

=6.5，

a

=

.

y

-b

.

x

=50-6.5×5=17.5…（11分）
因此回归直线方程为

y

=6.5x+17.5；…（12分）
（3）x=10时，预报y的值为y=10×6.5+17.5=82.5（万元）．…（14分）

点评：本题考查回归直线方程的求法，散点图的画法，回归直线方程的应用，基本知识的考查．